雪の結晶は、なぜ六角形？ 天からの手紙を解読した2人の博士

もうすぐクリスマス。今年のクリスマスは、ホワイトクリスマスとなるでしょうか。
ホワイトクリスマスといえば、ちらちらと舞う雪が素敵ですが、みなさんは雪の結晶を見たことがありますか。繊細で華麗な雪の結晶の美しさには、だれしも魅了されてしまいますね。今回は、美しい雪の結晶の構造に迫りながら、雪の結晶に魅せられた先人たちの足跡をたどっていきたいと思います。

雪の結晶の分類

繊細で美しい形が魅力的な雪の結晶は、「氷晶」と呼ばれる氷の結晶を核にして、まわりにある水蒸気を取り込んで成長したもののことをいいます。この成長のことを「昇華成長」といいます。氷晶は、気体である水蒸気が固体になったもので、昇華成長のしかたによって、いろいろな形の雪の結晶が生まれます。

では、雪の結晶の形をいくつか紹介しましょう。

     
雪の結晶と聞いて、多くの方が思い浮かべるのは六花の形をした扇状や樹枝状でしょう。とても美しいですね。ただ、これらは他の形状と混ざり合っていることが多く、分類が難しい場合もあります。

なぜ六角形なのか？

樹枝状の雪の結晶は、六角形が基本の形になっています。では、なぜ六角形なのでしょうか。
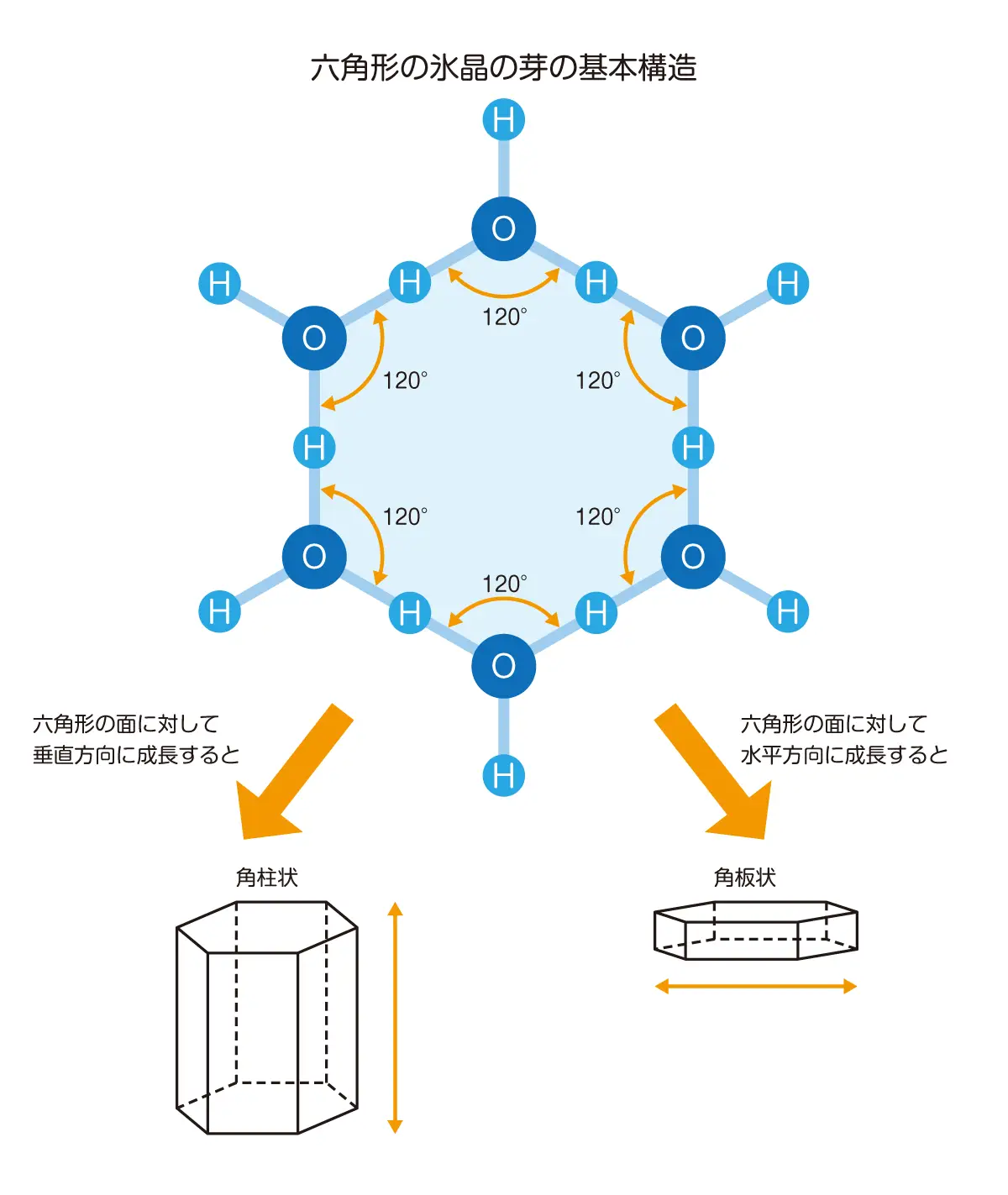
先ほどご紹介した昇華成長について、原子・分子の世界で見てみましょう。水分子（H₂O）は、１個の酸素原子（O）と２個の水素原子（H）が結合角^※1104.5°の構造になっています。氷晶は、水分子同士が水素結合^※2することで生まれます。ある水分子の酸素原子と、他の水分子の水素原子がくっつくわけですね。
※1結合角…１個の原子が２個の原子と結ばれるとき、それぞれの原子間を結ぶ直線のなす角のこと。
※2水素結合…分子のなかにある水素原子（H）が仲立ちとなって、隣接する分子同士が引き合う結合のこと。

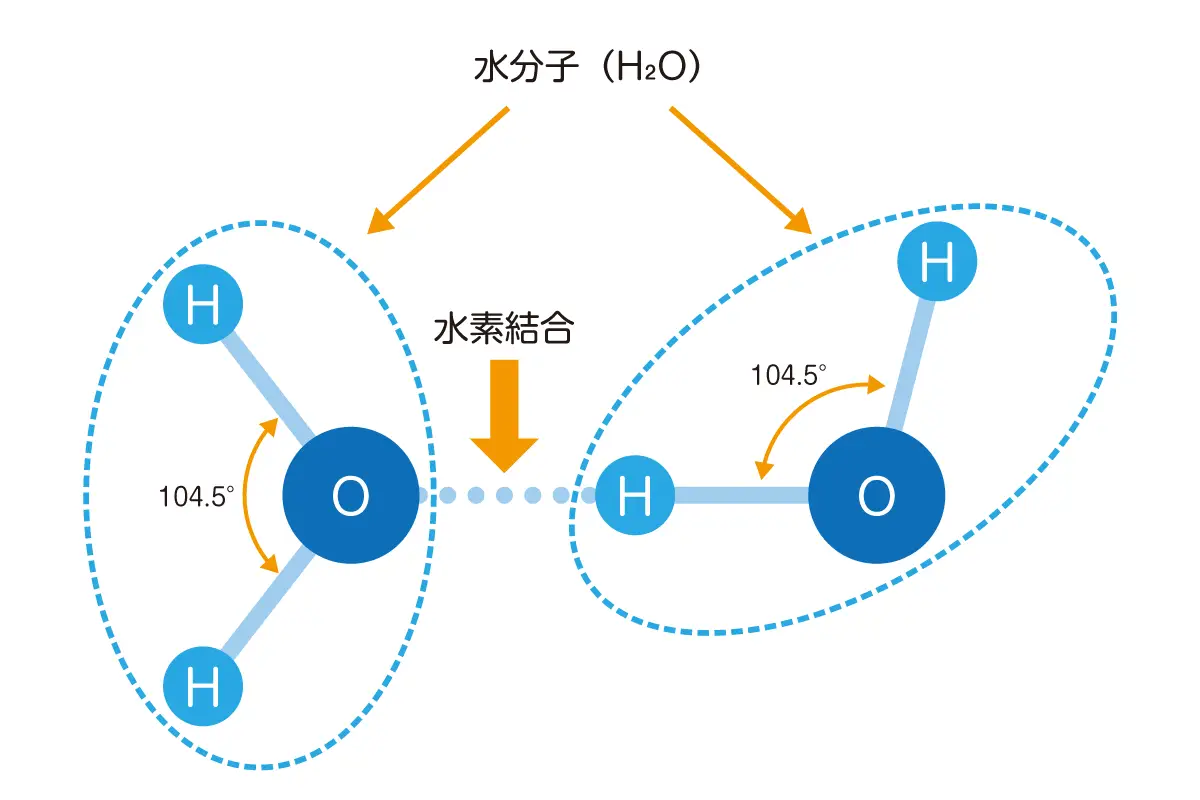
氷晶のまわりにある水蒸気が昇華してさらにくっつく（水分子（H₂O）が他の水分子とどんどん水素結合する）と、酸素原子（O）にくっついた３個の水素原子（H）同士がバランスを保ち、結合角が120°で結合して六角形の構造になるのです。この六角形の氷晶の芽が成長すると、いろいろな形状の雪の結晶になります。たとえば六角形の面に対して垂直方向に成長すると角柱状に、六角形の面に対して水平方向に成長すると角板状になります。

天からの手紙を受け取った2人の博士

雪の結晶にはさまざまな形があることをご紹介しましたが、「雪の結晶の形状を決める条件は何か」を調べるため、観測や実験を行ったのが中谷宇吉郎博士（1900～1962）です。雪の結晶の美しさに魅せられて研究者になった有名な学者です。中谷博士は、北海道帝国大学（現在の北海道大学）の構内に人工雪を作る低温室を建て、実験を行いました。この人工雪を作った実験場所の跡地に立っているのが、「人工雪誕生の地」の記念碑です。

中谷博士は、雪の結晶が成長する温度と水蒸気量、つまり湿度を変えるとどんな形状に成長するかを研究し、「中谷ダイアグラム」を作成しました。中谷博士は、中谷ダイアグラムを得る過程で「雪は天から送られた手紙である」という言葉を残しました。地上に舞い降りてきた雪の結晶という手紙を読むことで、結晶が成長した上空の温度や湿度が推測できると語っているのです。
その後、中谷博士の実験を引き継いだのは、小林貞作博士（1925～1987）です。彼は、より精度の高い実験を行いました。この実験結果をまとめたのが「小林ダイアグラム」で、以下の図は一部簡略化しています。

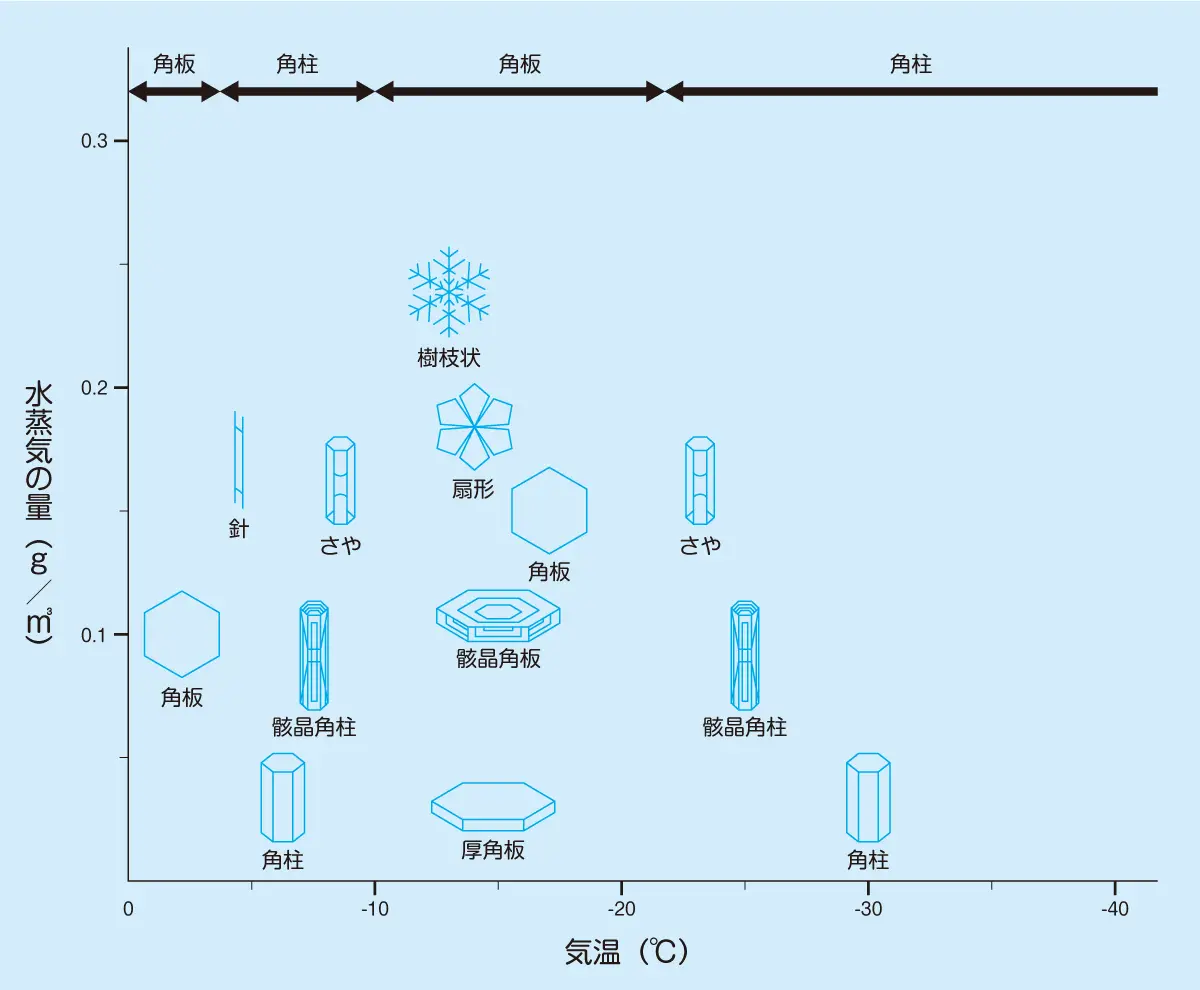
縦軸は水蒸気量を表しており、上側ほど水蒸気量が多く（湿度が高く）なっています。横軸は温度で、右側ほど低温を表しています。中谷ダイアグラム、小林ダイアグラムとも、水蒸気量（湿度）と温度がどのようなとき、雪の結晶がどんな形状に成長するかを表しています。たとえば、－10℃から－20℃では、水蒸気量が増加するにつれて基本の六角形から、厚角板→骸晶（がいしょう）角板→角板→扇形→樹枝状に成長・変化することがわかります。なお、骸晶とは面にくぼみのある結晶のことです。

対称性の美学「群論」への誘い

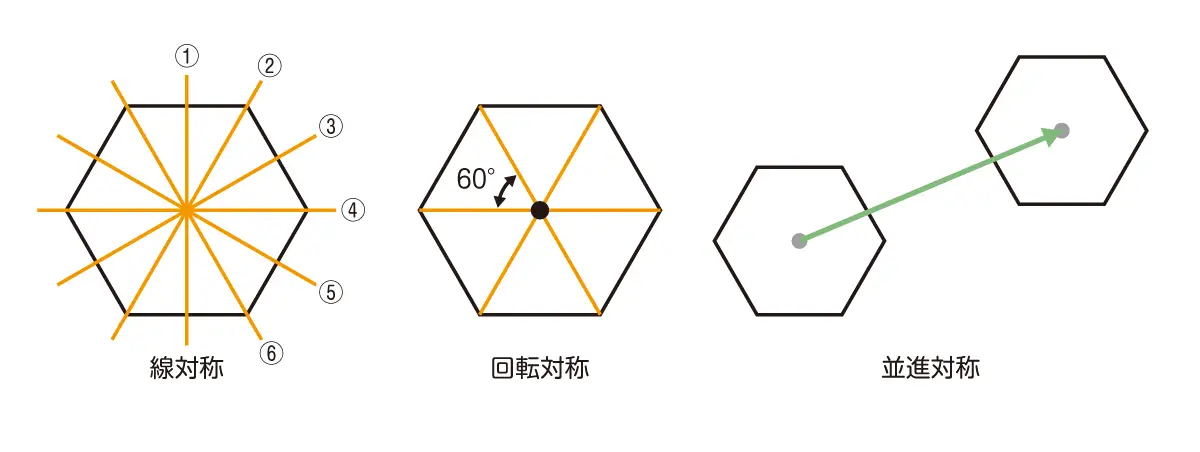
科学的な内容も交えながら、「雪の結晶」についてお話してきました。より数学的な視点で、雪の結晶の代表的な形状である六角形を正六角形と捉えると、対称性をもつことがわかります。下の図のように、正六角形は６本の対称軸をもつ線対称な図形です。また60°の角度で回転したときにもとの図形に重なる回転対称な図形であり、さらに平行移動したときにもとの図形に重なる並進対称な図形でもあります。

一般的に物質の結晶構造は対称性をもち、数学的には代数学の基本的な概念の１つである「群論」で扱うことができます。ダイヤモンドやエメラルドなどの宝石も、まさに結晶そのものです。植物の花弁、土星の環（わ）、建造物・美術品や工芸品といった創作物も対称性をもつものが多く、黄金比とともに様式美を決める要素の１つといえます。

今回は、「雪の結晶」の形の不思議についてお話ししてきました。雪が降ったときはみなさんの目でぜひ観察してみてください。そして、これをきっかけに創作物の美の世界、数学の「群論」へと、みなさんの興味・関心がさらに高まることになれば、うれしいかぎりです。

【参考文献】
中谷宇吉郎『雪』岩波出版（1994年）
菊池勝弘・梶川正弘『雪の結晶図鑑』北海道新聞社（2011年）
荒木健太郎『雲の中では何が起こっている：雲をつかもうとしている話』ベレ出版（2014年）
伊藤由佳理『美しい数学入門』岩波新書（2020年）
高橋礼司『対称性の数学　―文様の幾何と群論―』ちくま学芸文庫（2022年）