カレンダーのきまりを探そう

カレンダーは、日付の確認などのために使われ、とても重要で身近なものですが、実は数を利用した道具といえます。カレンダーのなかにはいろいろな「きまり」が隠れているのです。その「きまり」について考えていきましょう。

大の月、小の月を探そう！

カレンダーを見てください。1年は1月から12月までの12の月に分けられていますが、それぞれの月の日数は同じではありません。このことを計算で確かめてみましょう。1年は365日とすれば、365を12でわる計算を考えればよいですね。すると、

365÷12＝30あまり5

となり、すべての月を同じ日数にすることはできないことがわかります。

このことに対して昔の人は、月の大小という方法を考えました。大きい月と小さい月、つまり日数の多い月と少ない月をつくることで、1年間の日付を管理できるようにくふうしたのです。このくふうには、さまざまな科学的な調整や文化的な背景がみられます。日本では150年ほど前までは月の日数が毎年変わっていましたし、ヨーロッパでは1年の最後の月（当時は2月）で日数の調整を行っていました。現代のカレンダーに定まった経緯を親子で調べてみると、おもしろいかもしれませんね。

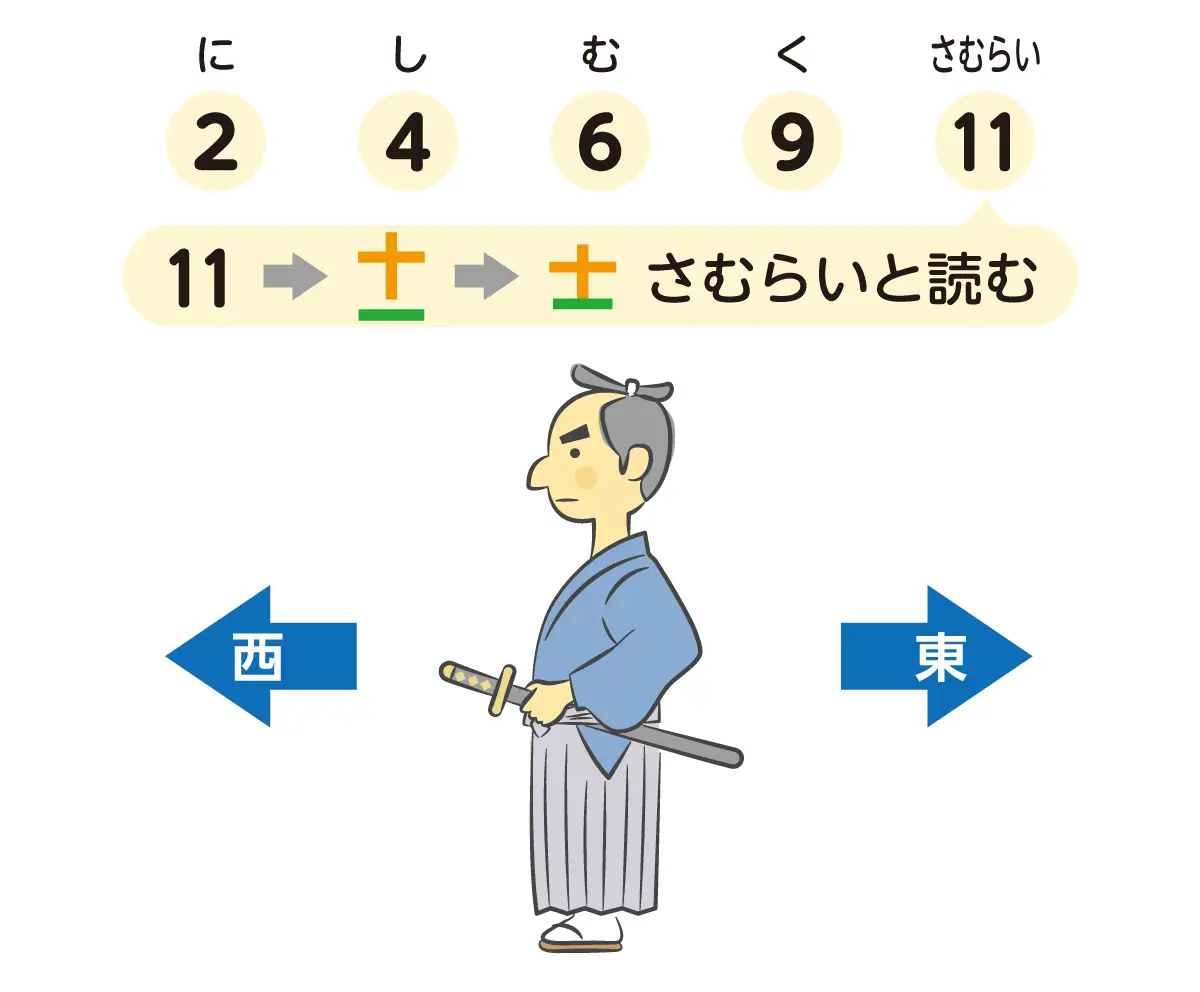
現代のカレンダーでは、大の月（31日）が1、3、5、7、8、10、12月の7か月で、小の月（28日または30日）が2、4、6、9、11月の5か月となっています。この1年の月の大小について「西向く士（にしむくさむらい）」と覚えている人も多いのではないでしょうか。これは、に（2）し（4）む（6）く（9）さむらい（11）という語呂（ごろ）合わせで、小の月の覚え方の1つです。「11」を漢字の「十一」にして「士（さむらい）」と読むなんて、何だかオシャレですよね。

月の日数がすぐにわかるようになると、スケジュールをたてるときなどに便利です。子どもとカレンダーをめくりながら、規則性や覚え方を話し合ってみましょう。

カレンダーはきまりの宝庫

カレンダーは規則正しく日付が並んでいますね。この数の並びを見て、いろいろなきまりを探してみましょう。

きまりを1つ挙げます。ある日付に着目すると、その上の日付は必ずもとの数から7をひいた数で、下の日付は必ずもとの数に7をたした数になっています。これは、どこの日付でも上の日付は1週間前、下の日付は1週間後で、7日間ずれているからですね。たとえば、10日に着目すると、上は10－7＝3（日）、下は10＋7＝17（日）となります。

これは縦に並んだ3つの日付の関係ですが、次にこの3つの数をたしてみます。3＋10＋17＝30となり、なんともとの日付の10の3倍になりました。関連して、横に並んだ日付を見てみましょう。10の左は９、右は11なので、これらをたしてみます。９＋10＋11＝30となり、またも、もとの日付の10の３倍になりました。

縦にたしても横にたしても3つの数の合計が真ん中の数の3倍になるのは不思議ですよね。

10日だから起きた偶然なのでしょうか。どこの日付でもそうなるのでしょうか。□を使って式で考えてみましょう。

縦にたした3つの合計は、真ん中の数を□とすると、

（□－7）＋□＋（□＋7）＝□＋□＋□＝□×3

横にたした3つの合計は、真ん中の数を□とすると、

（□－1）＋□＋（□＋1）＝□＋□＋□＝□×3□－1＋□＋□＋1＝□×3

となりますので、どちらもいつでも真ん中の数の3倍になることがわかりますね。□を使って考えると、発見した予想がいつでも成り立つかどうかを確認できますね。カレンダーのなかで縦や横に3つ並んだ日付の合計に関するきまりがわかりました。

それでは、10日を囲むように並ぶ9つの日付の合計はどのような数になるでしょうか。

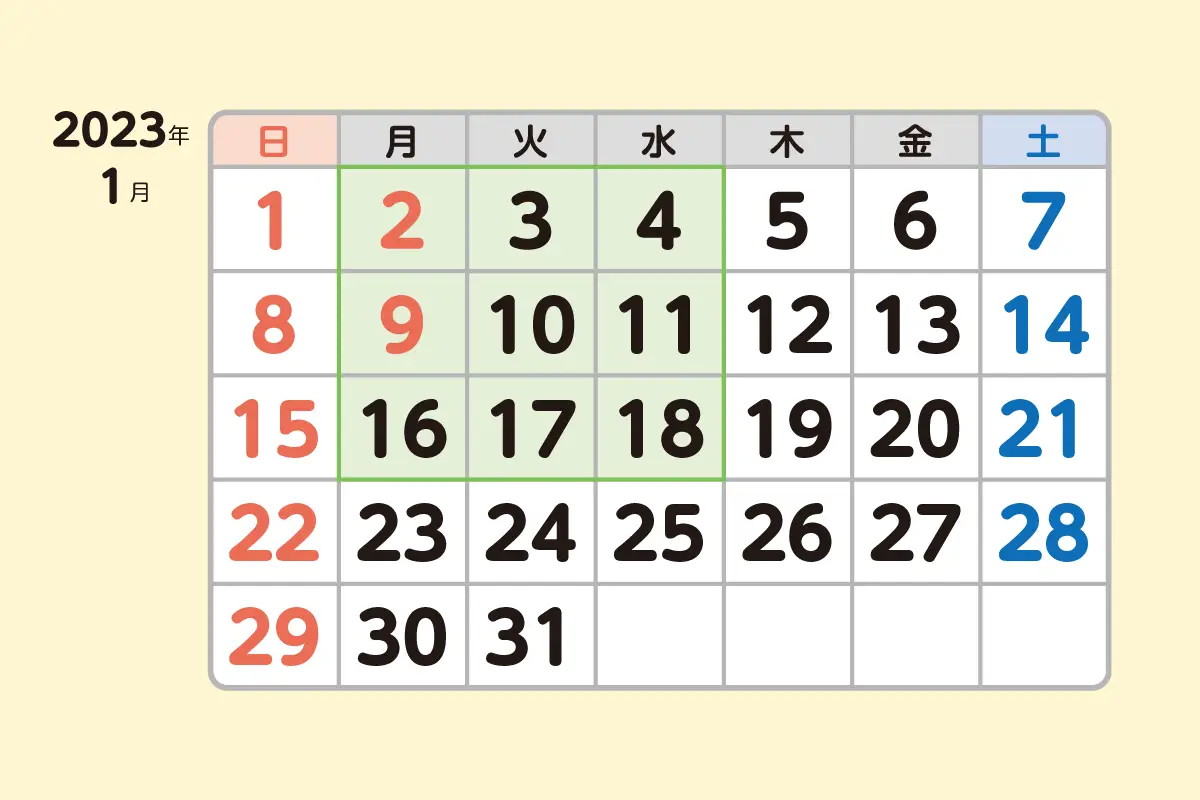
上のカレンダーを見ると、2＋3＋4＋9＋10＋11＋16＋17＋18＝90です。
真ん中の日付の10の9倍になっていることがわかりますね。

これも□を使って考えることができます。ぜひチャレンジしてみましょう。

曜日の不思議

月の大小についてお話しましたが、関連して、同じ曜日が5回の月と4回の月があります。曜日の回数について、どんなきまりがあるか考えてみましょう。

同じ曜日が何回あるかを求めるには、1か月のなかで1週間が何回繰り返されているかを求めればよいので、月の日数を週の日数でわればよいですね。大の月の日数は31日なので、31÷7＝4あまり3となります。

つまり4週間と3日ということですから、1日、2日、3日の曜日は5回あることがわかります。

小の月の日数は30日とすれば、30÷7＝4あまり2で、同じように考えると1日、2日の曜日は5回あります。

たとえば、1月1日が日曜日の場合、1月は大の月なので、日曜日、月曜日、火曜日が5回あり、それ以外の曜日は4回となります。

曜日の回数以外に、曜日と日付の関係にもきまりが発見できます。
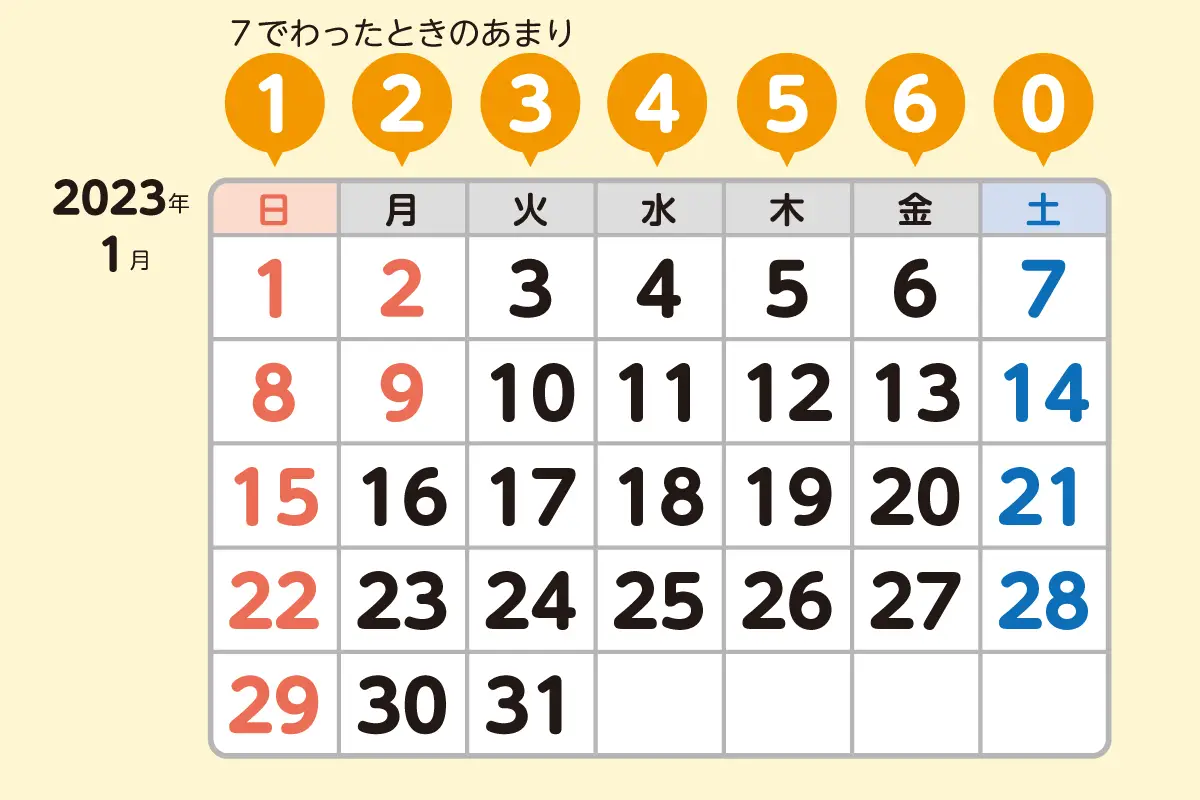
次のように、1月の日付を7でわったときのあまりに注目しましょう。

あまり0→土曜日
あまり1→日曜日
あまり2→月曜日
あまり3→火曜日
あまり4→水曜日
あまり5→木曜日
あまり6→金曜日

このように、あまりで曜日を分類すると、日付がわかれば曜日を求めることができます。

たとえば、1月4日は4÷7＝0あまり4で水曜日、1月15日は15÷7＝2あまり1で日曜日、1月26日は26÷7＝3あまり5で木曜日であることがわかります。

1年後は何曜日？

さて、ここで問題です。誕生日が1月8日で今年は日曜日だった太郎さんは来年の誕生日が何曜日か知りたくなりました。手もとに来年のカレンダーはありません。太郎さんの来年の誕生日は何曜日でしょうか。

1年は365日です。これを7でわると、
365÷7＝52あまり1
となり、52週間と1日となります。したがって、次の年の同じ日付では曜日は1日進みます。ですから、来年の太郎さんの誕生日は月曜日だとわかります。

しかし、曜日が2つ進むときもあります。それはうるう年のときです。うるう年は2月29日がある年のことで4年に1度あります。うるう年ではない年を平年と呼びます。つまり平年の日数は365日ですが、うるう年は1日多くなります。うるう年は1年が366日になるので、
366÷7＝52あまり2
となり、52週間と2日なので曜日が2つ進みます。

うるう年かどうかを考えて同じ日付の曜日を求めてみましょう。

太郎さんの誕生日（1月8日）は、次のように曜日が変わっていきます。

2023年1月8日（日）平年
2024年1月8日（月）うるう年
2025年1月8日（水）平年
2026年1月8日（木）平年
2027年1月8日（金）平年
2028年1月8日（土）うるう年
2029年1月8日（月）平年
2030年1月8日（火）平年

今年のように誕生日が日曜日になる年はなかなか来ないようですね。太郎さんの誕生日が日曜日になるのは何年後か、親子で考えてみましょう。

このように、カレンダーのなかにはたくさんの「きまり」があることがわかりました。計算もそれほど難しくありません。暗算で考えれば計算力の向上にも役立ちます。ぜひ、カレンダーを眺めていろいろな考察をしてみてください。

【参考文献】

平凡社編『改訂新版 世界大百科事典』平凡社（2007年）
四釜裕子・長尾美穂・内山さつき『12か月のきまりごと歳時記』自由国民社（2008年）

記事を書いた人

古山 竜司

大阪府生まれ。九州大学大学院卒業（芸術工学）。数学検定1級（数理技能検定）、英語検定準1級、数学コーチャープロA級ライセンス取得、ビジネス数学講師。「数学・算数を通じて人々を幸せにする」を使命に大阪府高槻市にマスラボを開業。またYouTuberとしても5,000本の動画を配信し、チャンネル登録者も1万人達成。著書に「これだけ微分積分」「これだけ微分方程式」（いずれも秀和システム）など。

算数・数学塾「マスラボ」
サイトURL：http://furuyaman.com/