アルキメデスは円周率をどうやって求めた？ 【偉人の方法を再現】

小学校の算数で習う「円周率」。「円周率 = 3.14」を知ることで、円周や直径などが求められます。

しかし「そもそも円周率ってなに？」「どうして3.14になるの？」と疑問をもつ方も多いのではないでしょうか。

今回は、そんな不思議な数「円周率」を巡る歴史をひもとき、実際に計算しながら円周率の奥深さを体験してみましょう。

円周率とは？

小学校の算数では、円周率の意味として次の式を習います。

円周率 = 円周÷直径

この式は、円周率がどういうものなのか教えてくれます。

「Ａ÷Ｂ」は、「ＡはＢの何倍か」を求める式です。このことから、「円周÷直径」は、「円周は直径の何倍か」を求めているということがわかります。

これを言い換えると円周率の意味がわかります。すなわち、円周率とは「直径に対する円周の比率」のことを指しています。

円は直径が変わることで大きさが変わりますが、どんな円でも形は同じですよね。そのため、どんな円でも直径と円周の比率は等しく、つまり円周率はつねに一定ということがわかります。

しかし円周率の意味はわかっても、

「直径と円周の比率は、なぜ 3.14 になるの？」

という疑問が生まれてくるのではないでしょうか。

これらの謎を解決するには、手を動かして “自分でやってみる” ことが大切です。ここからは実際に手を動かしながら円周率を求めてみましょう。

【体験】円周率を実際に求めてみよう！

歴史をさかのぼること約4000年前、円周率の歴史は紀元前2000年ごろの古代バビロニアでバビロニア人やエジプト人の計算から始まります。

今回はその歴史を振り返りながら、偉人のやり方で実際に円周率を求めてみましょう。

古代の方法に挑戦。実際に紙をくり抜いて考えてみよう

円周率がどのような円でも一定になることがいつ誰によって発見されたのかはわかっていませんが、約4000年前の古代バビロニア初期にはすでに、円周率を「3」として円の面積などが計算されていました。

その後、もっと正確に求めようと多くの人が挑戦する過程で、円とひもを使って円周と直径を測る方法が生み出されました。

それでは、実際にやってみましょう。

【用意するもの】 ・紙 ・コンパス ・はさみ ・ひも ・定規 ・セロハンテープ 【手順】 ①直径の長さを決め（今回は12cmで作成）、コンパスで紙に円をかきます。 ②かいた円を、はさみを使って紙からくり抜きます。 ③くり抜いた円の周囲にひもを巻き付け、ちょうど1周したところでひもを切ります。 ④切り取ったひもを真っすぐにして、長さを測ります。 ⑤「円周÷直径」を計算します。すると……？

計算の結果はいくつになったでしょうか。その値が円周率です。

古代の人々は、このような円周と直径を実測する方法で「円周率 = 3.125 」とわりだしました。円周率を「3」としていたころよりも正確にわかるようになったため、建築などの分野で活用されたそうです。

アルキメデスの円周率の計算方法をやってみた！

「計測」をもとに円周率を調べていた時代から、人々は円周率を「計算」で求めようと研究しました。はじめて計算で円周率を導き出したのが、古代ギリシャの数学者アルキメデスです。

アルキメデスは、

「円に対し、その内側と外側にぴったり接する多角形をかくと、円周は『内側に接する多角形の周の長さ』より長く、『外側に接する多角形の周の長さ』より短くなる」

「頂点の数を増やして円に近い正多角形を使えば、より正確な値まで円周率の大きさを絞り込める」

と考えました。

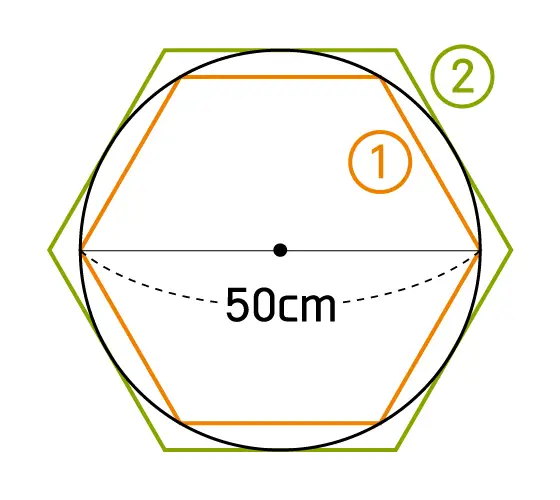
ここでは、正6角形と正12角形の場合を例に考えてみましょう。

※アルキメデスは、正多角形の周の長さを計算で求めたとされていますが、少し難しいため、ここでは実際に測った長さを用いることとして、アルキメデスの考え方に焦点を当てていきます。

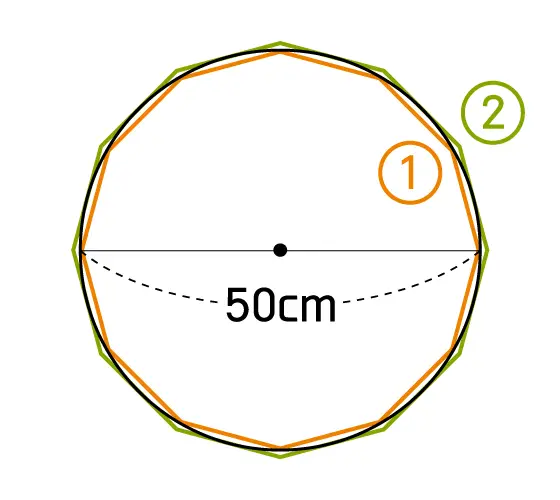【円の直径が 50cm、正12角形の場合】 ①内側に接する正12角形の周の長さ： 155cm ②外側に接する正12角形の周の長さ： 161cm 正6角形の場合と同じように、範囲を表すと、  155＜50×円周率＜161 となります。3 つの値をそれぞれ 50でわってみましょう。  3.1 ＜ 円周率 ＜ 3.22 正12角形を使った場合、円周率は「 3.1 より大きく 3.22 より小さい」という範囲まで絞り込めました。

正6角形より正12角形の方が、円周率の値の範囲が絞り込まれていますね。

アルキメデスは、この計算になんと「正96角形」を使いました。そうして導かれた結論は「円周率は 3\(\tfrac {10}{71}\)  より大きく 3\(\tfrac {1}{7}\)  より小さい」というものでした。小数になおすと「3.1408…＜円周率＜3.1428…」となるので，小数第２位まで正しく求められていることになりますね。

円周率は不思議な数。算数・数学をもっと楽しもう！

アルキメデス以降の数学者も、より正確な値を求めようと、円周率の計算に挑戦しました。円周率の求め方にはいろいろな方法があるので、調べてみるとおもしろいですよ。

その後、スーパーコンピュータの出現により、計算の精度は飛躍的に高まりました。競うように計算が進められ、1949年には2037桁、1973年には100万桁にまで到達。現在では 62兆8000億桁まで求められています（2021年8月現在）。

円周率は一見単純に思える数ですが、今日のように高い精度で導き出されるまでには、長い歴史と数多くの数学者たちの努力がありました。歴史を知り、偉人たちと同じ方法で実際に手を動かしてみたことで、今までより少し深く、円周率のおもしろさや不思議さを感じていただけたのではないでしょうか。

公式や数をそのまま暗記するだけでなく、実際に体験することで、算数・数学を楽しんでみましょう。

（参考文献）

講談社ブルーバックス 「2000年間も数学者を苦しめた「3つの難題」挑戦してみませんか？」（参照：2022-01-27）

地域教材社「円周率を求めて」（参照：2022-01-27）

ZDNet Japan「円周率計算で世界記録を大幅更新、スイス研究チームの高性能コンピューター」（参照：2022-01-27）