微分・積分をざっくり理解！身近な事例３選も紹介

高校数学のなかでも、とくに難しくつまずきやすいといわれる微分・積分。記号や数式などの複雑さから、なじみにくいものと感じる方も多いのではないでしょうか。

しかし、微分・積分は私たちの生活のあらゆる場面で活躍する「なくてはならない発明」なのです。基本的な考え方と身近な事例をもとに、そのおもしろさをひもといてみましょう。

すでにあなたも使っている「微分・積分」

まずは、微分・積分がどのようなものかをみていきましょう。イメージをつかむために、算数で登場する「距離」「時間」「速さ」の関係にあてはめて解説します。

微分は「細（微）かに」「分けて」考える

微分は「細（微）かに分けて考える」ことで、ある一瞬の変化をとらえるための方法です。

たとえば、ある自動車が1時間に50km進んだとします。この自動車の速さは「速さ=距離÷時間」の式から、時速50kmと求められます。

このように進んだ距離とかかった時間がわかれば、「速さ」という１つの値を導くことができます。しかし実際には、止まっているところから次第に加速したり、道路や歩行者の状況にあわせてスピードを調節しながら走ったり、やがて減速して信号で止まったり……と、その速さは一定ではなく１時間のなかで変化していたかもしれません。算数で習う「速さ」は、あくまでも「平均の速さ」といえるのです。

でも、実際の自動車にはスピードメーターがついていて、刻一刻と変化する速さをちゃんと表示していますよね。

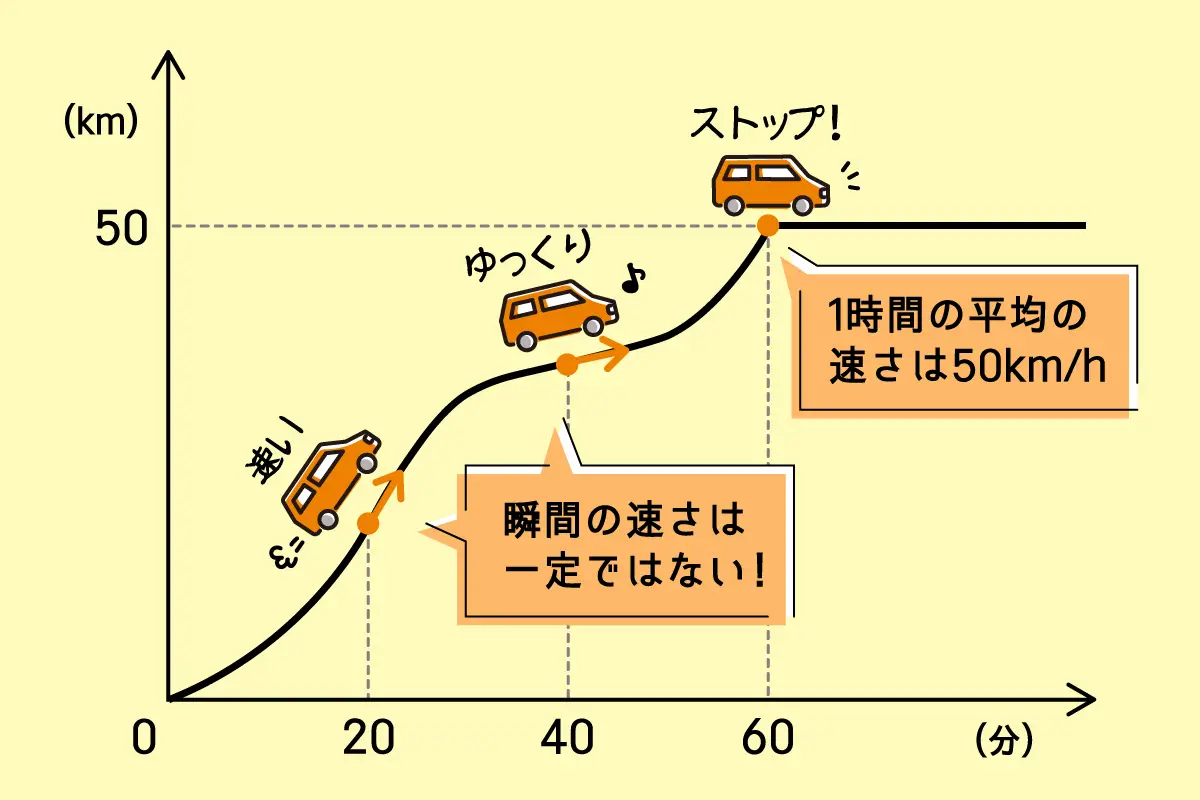
では、この自動車がある一瞬、ほんのわずかな間に出していた速さを求めるにはどうしたら良いでしょうか。

「距離」「時間」「速さ」の3要素のうち「時間」を限りなく０に近づけ、そのわずかな時間に進んだわずかな距離を「距離」にあてはめると、

（瞬間の速さ）=（ほんのわずかな距離）÷（ほんのわずかな時間）

といえますね。この「瞬間の速さ」は「変化を細（微）かに分けて考えたもの」であり、こうした小さな変化をくわしく調べることを「微分」というのです。

積分は「分けた」ものを「積んで集めて」考える

積分は「分けたものを積んで集めて考える」ことで、ある一瞬の変化をあわせて全体の量をとらえるための方法です。つまり、微分とは反対の意味を持つ考え方といえます。

微分と同じように、速さを例に考えてみましょう。ある自動車が１時間走っている間を３つの区間に分けて速さを調べたところ、「最初の30分は時速60km、次の20分は時速35km、最後の10分は時速50kmで走っていた」とわかったとします。

この自動車が１時間で走った距離を求めてみると……「距離=速さ×時間」の計算式から、最初の30分で30km、次の20分で11.7km、最後の10分で8.3km進み、全部で50km進んだことがわかります。

このとき、それぞれの区間における自動車の速さはあくまで「平均の速さ」なので、それぞれの区間のなかで速さが変化している可能性があります。速さを大まかにとらえているので、その速さをもとに計算した距離も、大まかな値になりますよね。

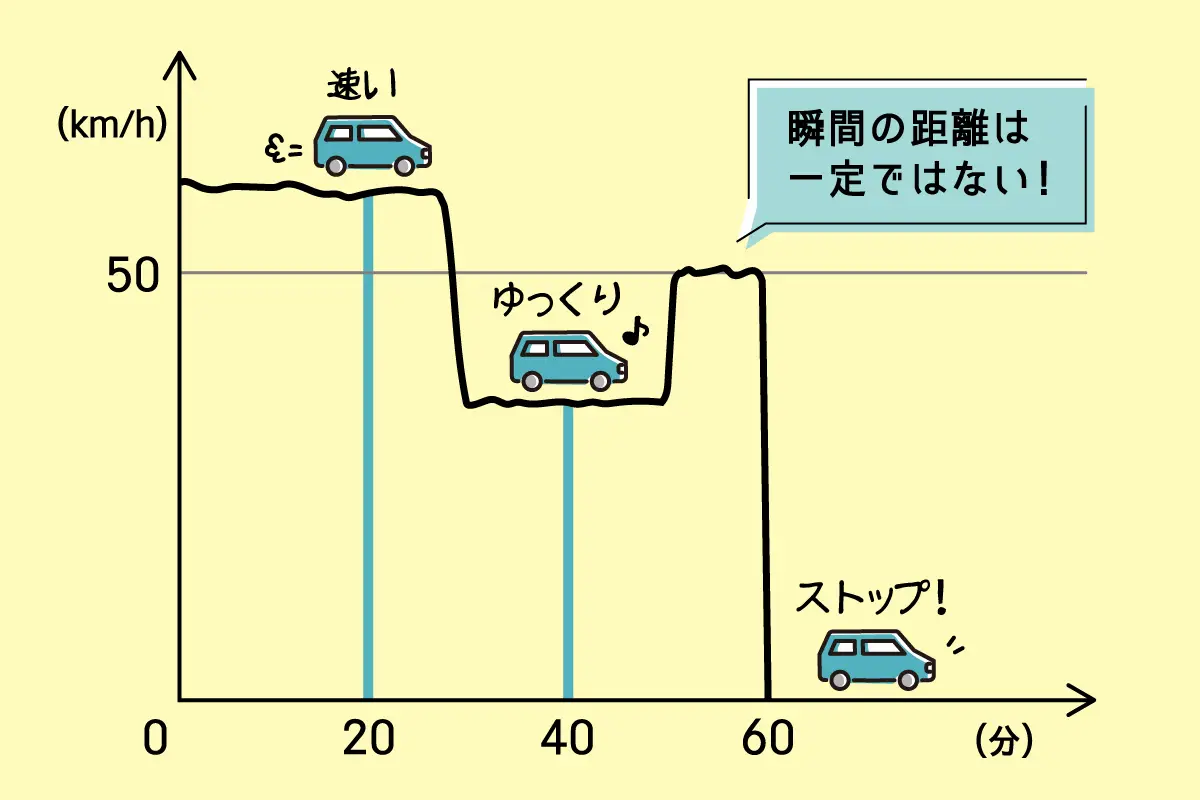
では、走った距離をより高い精度で求めるにはどうしたら良いでしょうか。

１時間走行した間の速さの変化を「10分間」や「20分間」といった広い間隔ではなく、限りなく細かな間隔でとらえ、

（瞬間の速さ）×（ほんのわずかな時間）＋（瞬間の速さ）×（ほんのわずかな時間）＋…… ＝（確からしい距離）

とすべてをあわせれば、限りなく精度の高い距離が求められます。この「確からしい距離」は「細かく分けたものを積んで集めて考えたもの」であり、こうした小さな変化を総合して全体的な量を求めることを積分といいます。

【こんなにある！】身のまわりの「微分・積分」

微分・積分のイメージがつかめてきたところで、この考え方が日常のどのようなところで使われているのかみてみましょう。きっと、難しい計算も今までより少し身近に感じられるはずです。

天気予報

とくに身近な例として、日々私たちに届けられる天気予報があります。天気予報では、微分を使って気温や風、湿度といった大気の状態の「瞬間の変化率」を導き出し、一定の時間がたったあとの変化量を積分によって解析することで、その後の天候が予測されます。

実は、この予測方法が生まれる前の天気予報は、天候と空模様のパターンをみつけることで翌日の天気を予測する、経験に頼った不確実なものでした。微分・積分の考え方が取り入れられるようになったことで、かつての天気予報と比べて予測の精度が飛躍的に高まったのです。

スマートフォンのバッテリー残量

スマートフォンのバッテリー残量の計算には、積分が使われます。スマートフォンは画面をロックして使っていないときもあれば、動画視聴や誰かと連絡を取るために使うときもありますよね。つまり、消費する電力の量は一定ではなく、その時々によって変化しています。

そこで「時間によって変化する電流の値を積んで集めて考える」ことで、すでに使った電気の総量をより精度高く求め、確からしい残量を導くことができるのです。

自動車の走行距離メーター

はじめの例でご紹介したように、速度が一定ではない自動車が実際に走った距離を測るために、積分が使われます。自動車の走行距離メーターに表示される数値は、自動車が走り続けてきた間の速度の変化を限りなく細かな時間の間隔でとらえ、「ほんのわずかな時間の間に進んだ距離」をすべて足しあわせて求められた、限りなく精度の高い「距離」なのです。

微分・積分がなかったら世界は中世のまま！？

微分と積分では発展してきた歴史が大きく異なりますが、17世紀ごろに両者のつながりが発見され、現代に通ずる微分積分学が確立されました。現在では、これまでに挙げた天気予報、スマートフォン、自動車用メーターのほかにも、以下のような例をはじめとして数え切れないほどの領域で微分・積分が使われています。

• 楽器の設計

• 建物の強度の計算

• 橋など構造物の安全性の計算

• 人工衛星の軌道の計算

• 経済の変化の予測

• ウイルスの感染拡大のシミュレーション

微分・積分の発明によって数学が発展したことが、物理学とそれにともなう工業の発展、ひいては経済の発展につながり、私たちの暮らしを豊かにしています。

安全な建物や橋などの構造物が立ち並ぶ街で暮らし、遠距離であっても飛行機で便利に移動ができ、コンピュータやスマートフォンを使って自在にコミュニケーションが取れる……、このような現代の暮らしは微分・積分に支えられています。もしも微分・積分が今も発明されていなかったとしたら、私たちの暮らしは中世から発展しないままだったかもしれません。

微分・積分の考え方は武器になる

私たちの生活には「数学」の活躍が欠かせません。数学の知識や考え方を身につけることは、社会生活を営むうえで大きな武器になります。ここまでみてきた微分・積分を知ることがどのような武器になりうるか考えてみましょう。

ロジカルシンキングが身につく

自動車走行距離メーターには、「車自動車の速度が絶えず変化していることから、走った距離を単純に“速さ×時間”で求めることができない」→「細かに分けた距離を積んで集めて考えよう」という積分の発想が使われています。

このように物事の特徴をとらえ、解決への見通しを立てる発想は、ロジカルシンキングにもつながります。数学だけでなく、合理的な判断や説得力のある説明が求められる場面でも役に立つでしょう。

コミュニケーションの幅が広がる

建物の強度や橋などの構造物の安全性は、微分・積分を使うことによって“数字で”“定量的に”表せます。「この橋はがんじょうなので安全です」と性質だけにフォーカスするのではなく、「橋の強度は◯◯で、この数値は安全基準を満たしています」と定量的に表現することで、より説得力が高められますね。

物事を定性・定量の両面からとらえ、その解釈を数学的に表現することで、相手にわかりやすく伝えることができ、コミュニケーションを取りやすくすることにもつながるのです。

世の中のしくみがわかる

先人たちが世の中の物事を数・量・図形に着目して観察し、「より良い方法はないか」と批判的に考察して解決策を考えてきたことで、現代の“便利さ”が広まりました。

また、観察した数や量の変化をもとに天気や経済、ウイルスの感染拡大状況など未来を高い精度で予測することも可能になりつつあります。

数学を理解することは、このような先人たちの発想や世の中への貢献を知ることでもあるとともに、同じような発想・構想の力を身につけて世の中のしくみを正しくとらえることにもつながるでしょう。

身のまわりには「算数・数学」がいっぱい！

ふだんあまり意識することはないかもしれませんが、身のまわりには微分・積分をはじめとする数学的な考え方があふれています。そうした数学的な考え方に触れることで、世の中をより正確に理解することができるでしょう。

まずは身のまわりの事例をみつけ、それに使われる原理や発想を少しずつひもときながら、数学を楽しんでみませんか？