「割合の計算」の解き方｜算数単元別解説

今回は算数の単元「割合」について、問題の解き方を解説するとともに、考え方のポイントをご紹介します。

割合の問題では、書かれている内容を読み解き、出てくる数値の関係を整理しながら式を組み立てていく過程がつまずきやすいポイントです。公式を丸暗記して問題を解くのではなく、まずは基本となる考え方を理解し、計算を頭のなかでイメージするように解いていきましょう。

【そもそも】割合とは？

割合とは、ものの量や大きさなど、２つの数量の関係を示す、「あるものの量がもう一方の量の何倍にあたるかを表す数」です。

スポーツチームが全試合のうちでいくつの試合に勝ったかを表す「勝率」、ある品物がもとの値段からどのくらい値引きされるかを表す「割引率」など、割合の考え方は私たちの生活で多く使われています。

割合のよさは、２つの数量の関係どうしを比べることが可能になることです。たとえば、勝率を用いれば、試合数が異なっていても、どのくらい勝っているかを比べることができますよね。

ここからは、割合の求め方と表し方をくわしくみていきましょう。

割合の求め方

割合は、次の式で表すことができます。

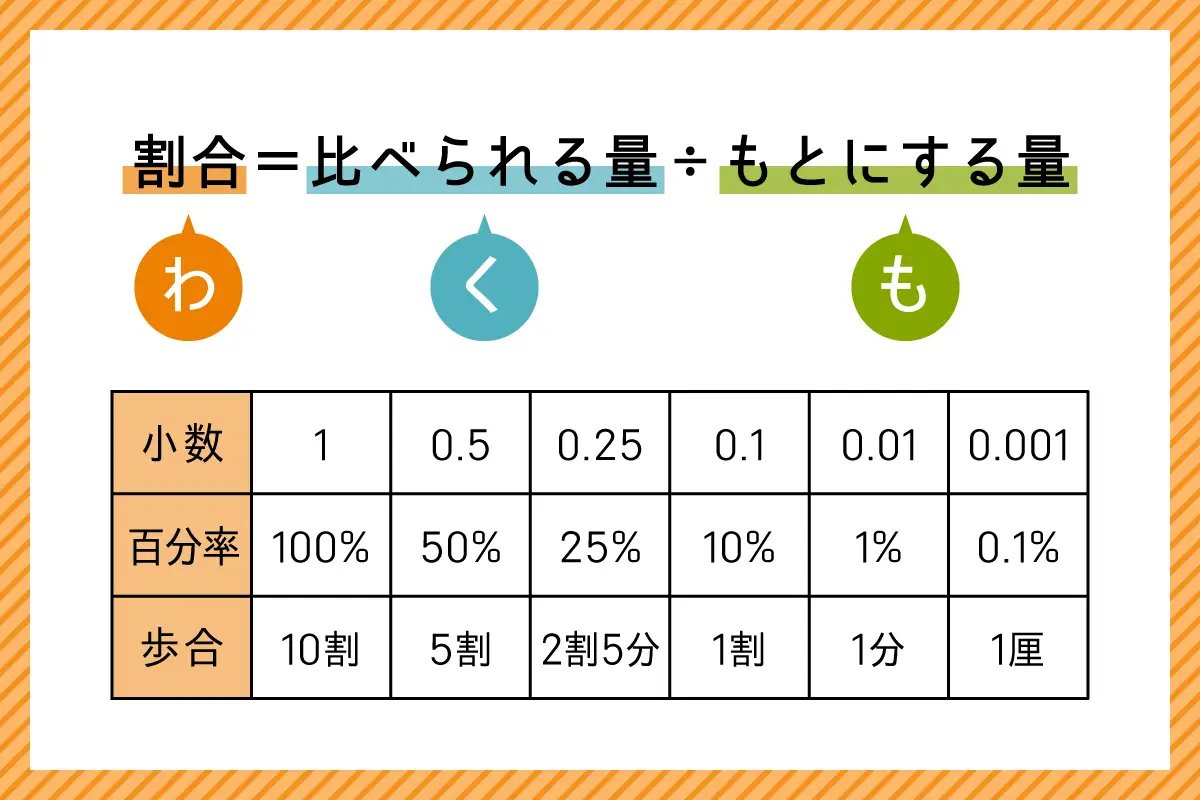
割合 = 比べられる量 ÷ もとにする量

割合を求めるためには、問題のなかから何が「比べられる量」で、何が「もとにする量」なのかを見極める必要がありますが、これは公式を覚えるだけでは難しいです。

何を基準にしているかを読み取ることについて、具体的な問題で確認してみましょう。

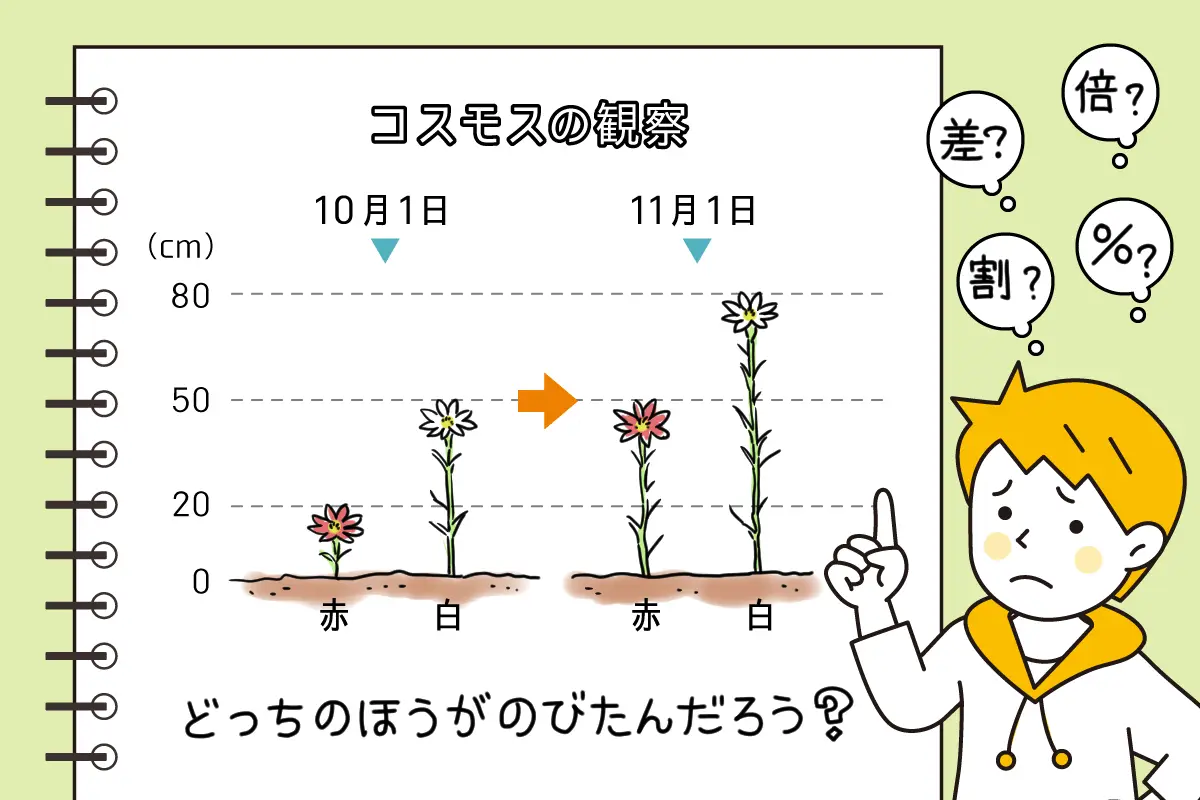
10月から11月の１か月間で、赤いコスモスは20cmから50cmに、白いコスモスは50cmから80cmにのびました。

問１　赤いコスモスは、１か月間で何倍になりましたか。

問２　２本のコスモスは、どちらのほうがのびたといえますか。

問１は、赤いコスモスが１か月間でどう変化したかを問われているので、「もとにする量」は10月の高さ、「比べられる量」は11月の高さとわかります。

式にして計算すると、

割合=比べられる量 ÷ もとにする量

= 11月の高さ÷10月の高さ

= 50 ÷ 20

= 2.5（倍）

とわかります。このように、問題文の文脈に沿って数量を読み取ることが大切です。

続いて問２を解いてみましょう。問題文を読むと２本のコスモスは、どちらも１か月間で30cmのびています。つまり、差で考えた場合どちらものび方は同じことになりますね。これは困った、いったいどうやって答えを求めればよいのでしょうか？

じつはそのヒントは「割合」にあります。

割合の公式に白いコスモスをあてはめてみると、

80 ÷ 50 = 1.6（倍）

赤いコスモスが2.5倍ものびたのに比べて、白いコスモスは1.6倍です。

よって、赤いコスモスのほうがのびたといえますね。

このように、２つの数量の間に比例的な関係があるときは、割合で比べてみるとわかりやすくなります。

割合の表し方【百分率（%）】

割合の表し方の１つに、百分率があります。百分率とは「もとにする量を100として、それに対する割合で表す」方法で、単位には％（パーセント）を使います。

たとえば、「20本のうち8本が当たりのくじ」で当たりの割合を求めます。全体のなかの部分について考えるときは、「もとにする量」が全体（20本）、「比べられる量」が部分（8本）となります。つまり、

8÷20＝0.4

と計算できます。これを百分率で表すと、

0.4×100＝40（％）

です。「何倍か」で表すときはもとにする量を1とみているのに対し、百分率で表すときはもとにする量を100としていることがポイントです。

割合の表し方【歩合（割、分、厘）】

百分率とあわせて覚えておきたい割合の表し方に、歩合があります。

歩合のなかでもよく耳にする「割」は、「もとにする量を10として、それに対する割合で表す」方法です。先ほどのくじの例で求めると、

0.4 × 10 ＝ 4（割）

となります。歩合の単位には「割」のほかに「分」「厘」があり、割合を表す0.01を1分、0.001を1厘といいます。昔の日本では1円未満のお金は「銭（1円＝100銭）」や「厘（1円＝1000厘）」という単位が使用されていました。こうした日本の歴史とあわせて考えると、歩合への興味もわくかもしれませんね。

割合の問題を実際に解いてみよう！

割合を求める式を用いる変形すると、割合に関するほかの量を求める式をつくることができます。

割合＝比べられる量÷もとにする量

比べられる量＝もとにする量×割合

もとにする量＝比べられる量÷割合

問題を解きながら確認していきましょう！

問題1. 割合を求める

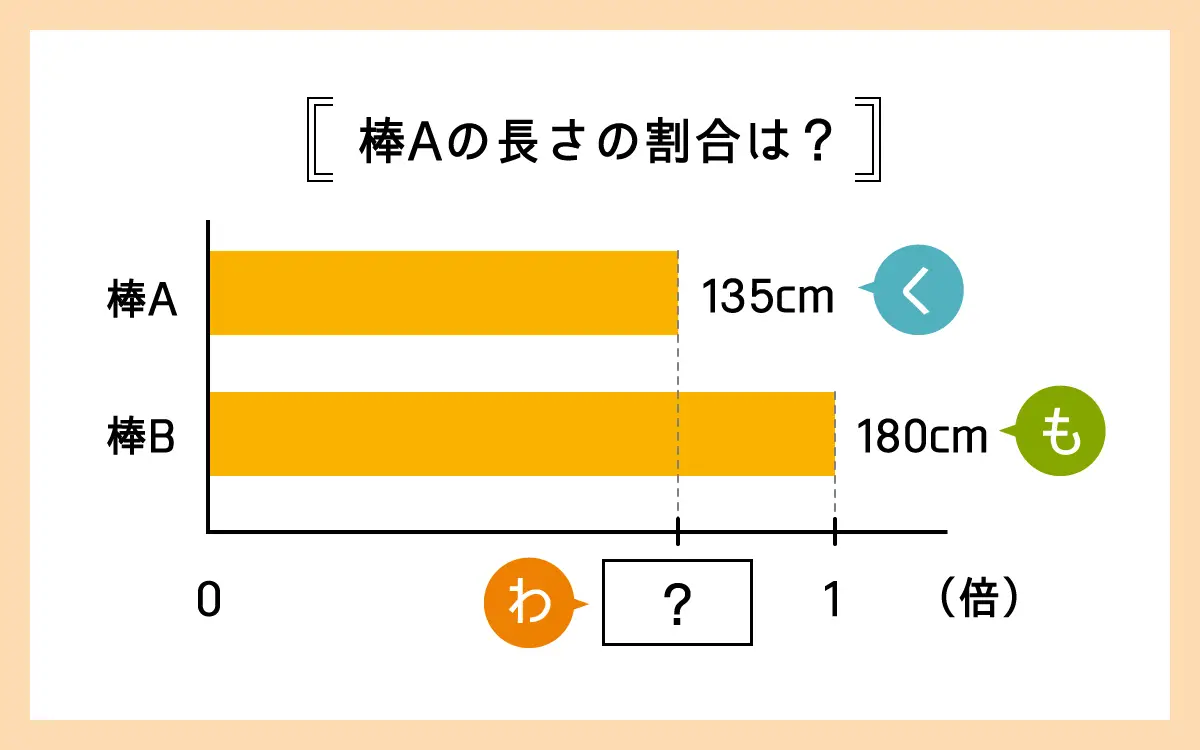
135cmの棒Aと180cmの棒Bがあります。棒Bの長さに対する、棒Aの長さの割合を求めましょう。

計算式は、

135÷180＝0.75

となります。この問題でも数量関係の読み取りが大切です。その方法の１つとして、図で整理するものを紹介しましょう。

下の図のように、それぞれの長さを可視化しながら問題文と対応させると、どのような数量なのか把握しやすくなります。この場面では、「もとにする量」は棒Bの長さ、「比べられる量」は棒Aの長さとわかります。

問題2. 比べられる量を求める

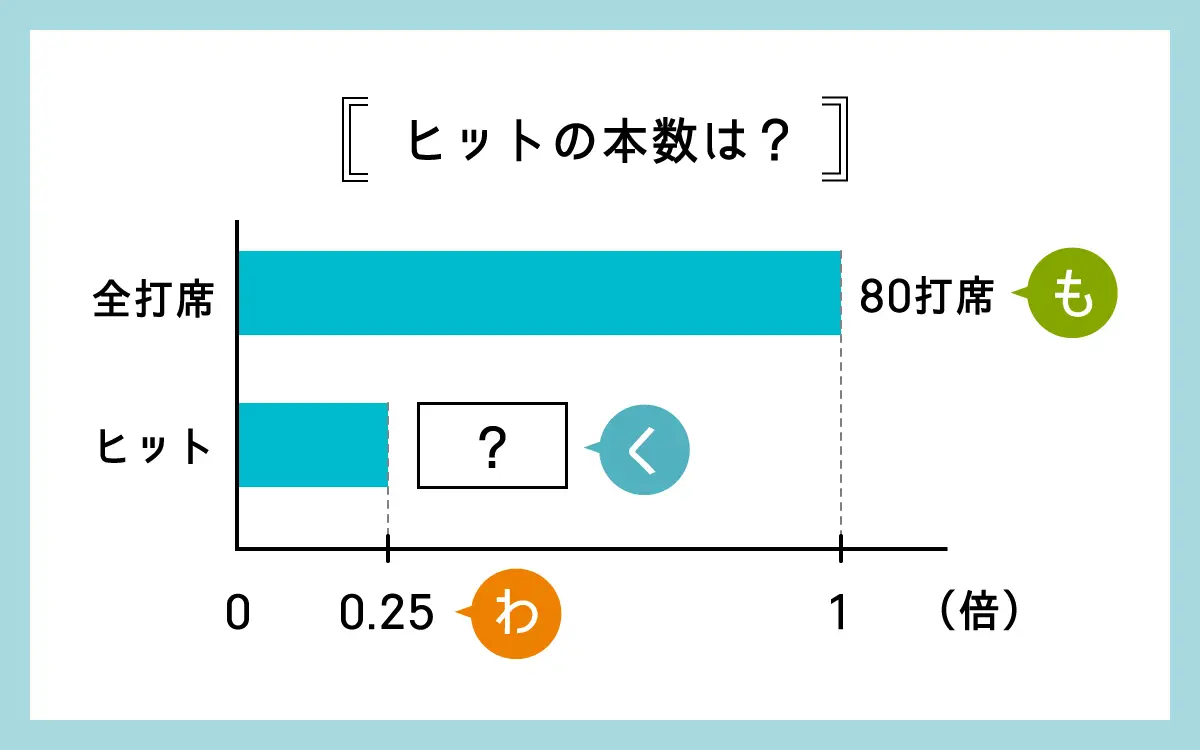
全80打席のうち、ヒットが25%だったとき、ヒットの本数を求めましょう。

まず、百分率を小数になおすと、

25÷100＝0.25

となり、計算式は、

80×0.25＝20（本）

となります。求めるものは割合ではないですが、先ほどと同様に図で整理することができます。下のような図をかいて、問題文の数量関係を把握しましょう。この場面では、「割合」は0.25、「もとにする量」は全打席数です。すると、求めるものが「比べられる量」だとわかります。

問題3. もとにする量を求める

陸上クラブの昨年の人数は、今年の人数の12割です。昨年の人数が24人のとき、今年の陸上クラブの人数を求めましょう。

歩合が登場しましたが，あせる必要はありません。

まず、歩合を小数になおすと、

12÷10＝1.2

となり、計算式は、

24÷1.2＝20（人）

となります。割合の基本的な問題としてはもっとも難しいパターンの問い方と思われます。

下のような図でどうでしょうか。この図より、「割合」は1.2、「比べられる量」は昨年の人数です。すると、求めるものが「もとにする量」だとわかります。

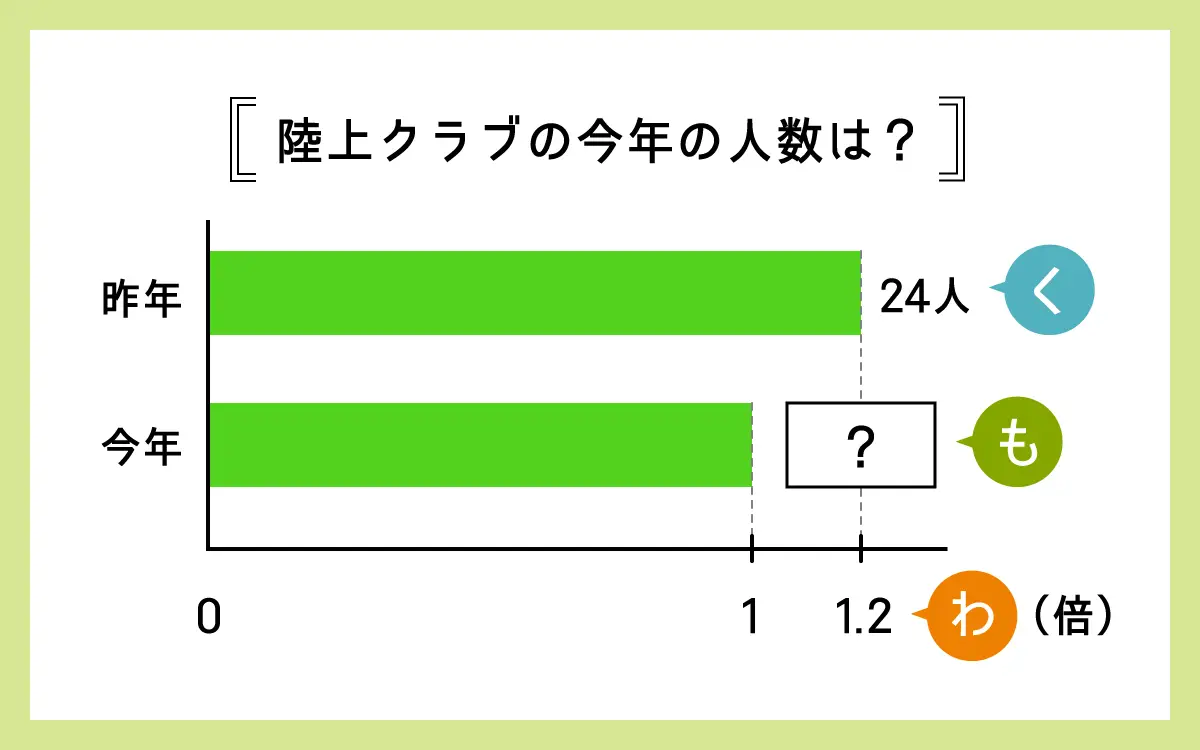
また、「昨年が今年の1.2倍」と読み取れたときに、「今年の人数は昨年より少ない」とわかることも大切です。答えのだいたいの大きさを見積もることができるので、計算の確認にもなるでしょう。これは割合に限らずいろいろな問題にいえることです。

【こんなにも】身のまわりの割合を探してみよう！

割合は、私たちの日常生活のにもたくさん隠れています。ここでは、割合の考え方が使われている3つの例をご紹介します。

買い物にかかる消費税

１つめの例は、買い物の場面でみられる「消費税」です。デパートやコンビニエンスストア、飲食店などで「本体3,000円＋税10％」「1,100円（税込）」「店内飲食なら消費税10%、テイクアウトなら8%」というような、さまざまな形の「税」にまつわる表記をみたことがあるのではないでしょうか。

「本体3,000円＋税10％」を例に考えてみましょう。この商品にかかる消費税が10%だった場合、商品本体の金額の10%が消費税として上乗せされます。

では、実際にこの商品を買う場合、いくら支払うことになるのか計算してみましょう。

まずは百分率で表された割合を小数の形に戻し、

10 ÷ 100 = 0.1 

とします。「消費税額は、本体価格3,000円の0.1倍」となるので、消費税額は、 

3000 × 0.1 = 300（円）

です。つまり、この商品の支払金額は、 

3000 + 300 = 3300（円）

となるのです。

このように消費税額を計算して本体価格にたす方法のほかに、支払金額と本体価格の割合を計算する方法でも同じ答えを求めることができます。

本体価格にその0.1倍の消費税が上乗せされるため、「本体価格に対する支払金額の割合」は

1 + 0.1 = 1.1

といえます。つまり「支払金額は、本体価格3,000円の1.1倍」なので、

3000 × 1.1 = 3300（円） 

と求められるのです。

割引セール

買い物の場面でみられるもう１つの割合の考え方に「割引セール」があります。「本体価格から3割引」「20%OFF」などのお得な表示についても、金額がどのように変化するのかみてみましょう。

たとえば、税込100円の商品がセールで「3割引」となっていた場合、支払金額はいくらになるでしょうか。

まずは歩合で表された割合を、小数の形に戻します。

3 ÷ 10 = 0.3

「割引額は、もとの価格100円の0.3倍」となるので、割引額は、

100 × 0.3 = 30（円）

です。つまり、100円から30円がひかれるため、この商品は70円で買えることになります。

また消費税の例と同様に、支払金額ともとの価格の割合を計算する方法でも同じ答えを導けます。

「割引率が0.3」ということは「もとの価格に対する支払金額の割合」は、

1 − 0.3 = 0.7

つまり「支払金額は、もとの価格100円の0.7倍」なので、

100 × 0.7 = 70（円）

となります。

野球選手の打率

野球観戦をする方は、「打率」という言葉を耳にしたことがあるのではないでしょうか？

打率は「打数に対するヒットの割合」を示す、バッターを評価するときに用いられる指標の１つです。

たとえば、あるバッターが「全74打数のうち、27本のヒットを打った」場合、「27本のヒットは、全74打数の何倍か」を求めるため、

27 ÷ 74 = 0.3648…

と計算し、四捨五入して打率は「0.365」となります。打率は一般的に「.365」と表されますが、歩合の考え方を用いて「打率 3割6分5厘」と表したり読んだりすることもあります。

まずは情報を整理しよう！

公式を丸暗記して割合の問題を解こうとすると、「もとにする量って？」「どちらが比べられる量？」とつまずきやすいもの。親子で問題を解くときは、問題文を読んで出てくる数値が何を意味するのかを一緒に整理し、数量の関係を頭のなかでイメージするようにうながしてみてはどうでしょうか。