その行列、並ぶ?待ち時間を「リトルの法則」で予測してみよう

大型連休が近づいてきましたね。「今年はどこかに出かけたい!」と思っている方も多いのではないでしょうか。
しかし、遊園地のアトラクションや有名なお店などの人気スポットは長蛇の列ということもよくありますよね。
それで「並ぼうかな、やめておこうかな」と悩んだり、決心して並んでも「いつ自分の順番が来るの?」とイライラしたり……。
そんな「行列」のお悩みやイライラは「リトルの法則」で解決できるときがあります!
この行列、何分待つの?
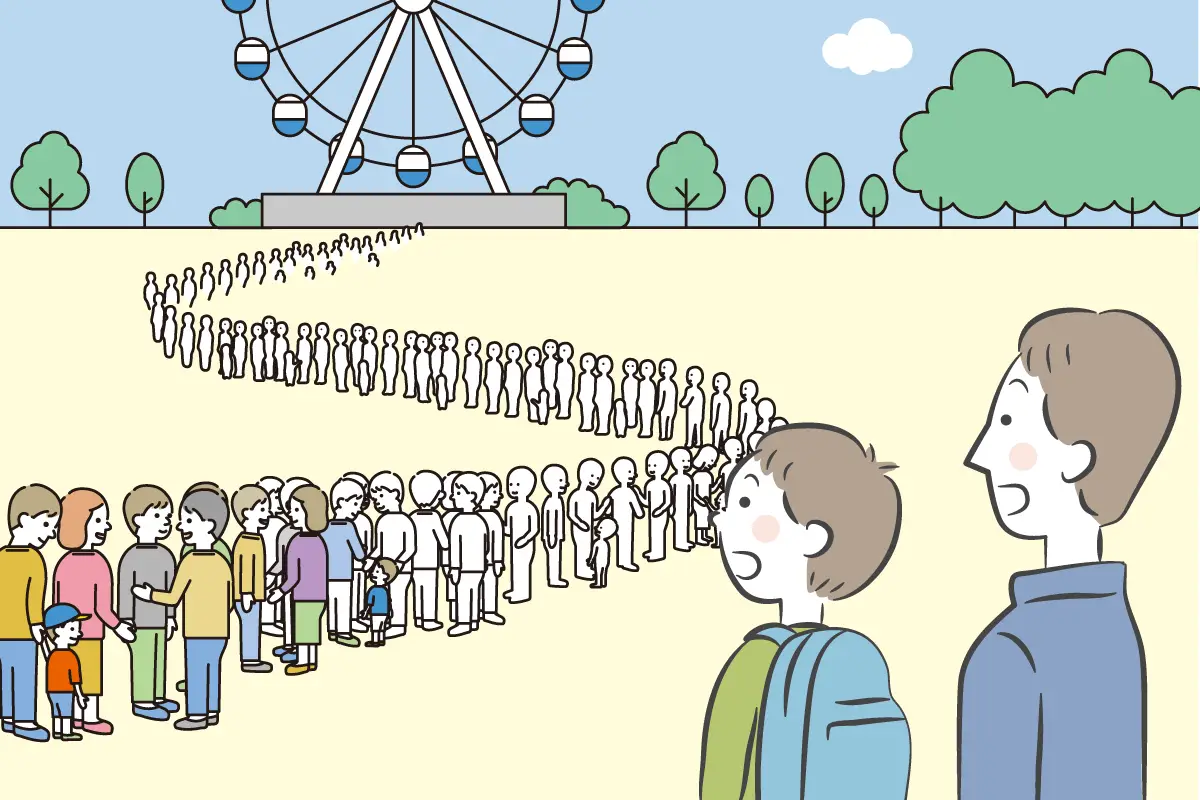
行列はどうしてできるのでしょうか?
多くの行列は、お客さんの人数が、サービスする側が処理できる人数(許容範囲)を超えたときにできるといえます。遊園地の観覧車に長い行列ができるのも、許容できる人数より多くの人が乗ろうとするからです。
こうしてできる行列に並ぶとき「待ち時間は何分くらいだろう?」って思いますよね。自分なりに計算したことがある人も多いのではないでしょうか。
たとえば「行列の長さを約10mとして、いま1分並んで2mぐらい進んだから、あと5分くらいかな」とか「1人の処理に約2分かかるとして、いま10人並んでいるから、あと20分くらいかな」などという計算ですね。
「待ち時間はどれくらい?」という、こうした疑問は昔から多くの人がもっていて「待ち行列理論」という研究分野があるくらい、さまざまな考え方があります。待ち行列理論では、おもに複雑な確率の考え方を用いますが、シンプルな公式ですぐに実践できるのが「リトルの法則」です。
リトルの法則とは
先ほどの例では、行列の長さを測ったり、1人分の処理時間を仮定したりする必要がありましたが、リトルの法則には不要です。この点について、リトルの法則であれば、1分待ってから行列に並ぶ人数をざっと確認するだけで使うことができます。
リトルの法則は、次のような公式で表すことができます。
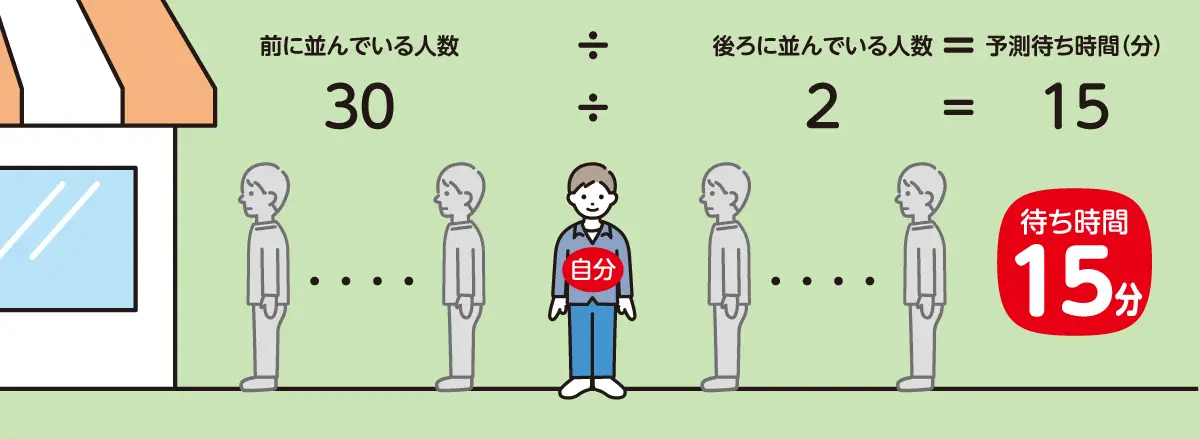
前に並んでいる人数÷後ろに並んでいる人数=予測待ち時間(分)
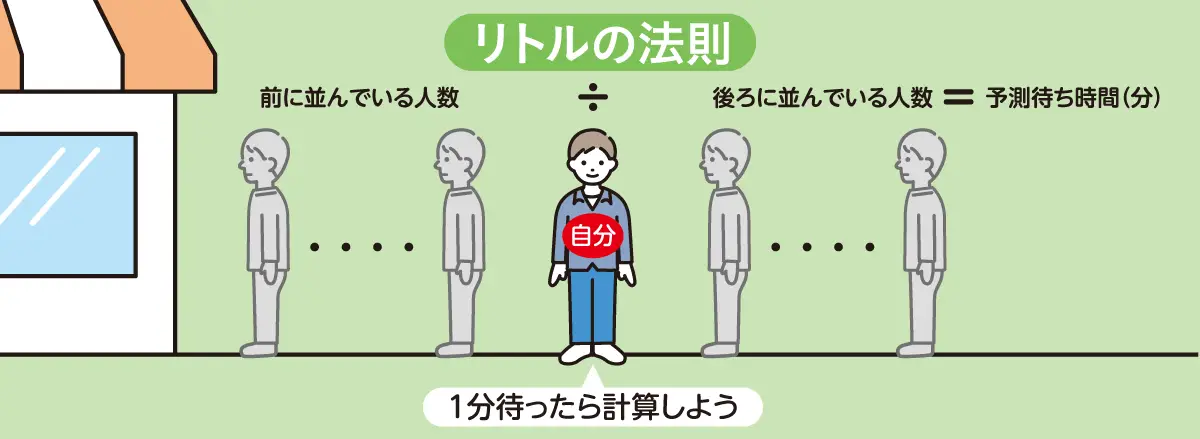
実際に求める場合は、次のような手順となります。
- 行列に加わり、1分待つ。
- 自分の前に並んでいる人数をざっくり数える。
- 自分の後ろに並んでいる人数を数える。
- (自分の前の人数)÷(自分の後ろの人数)を計算する。
この手順で、4の計算の答えが待ち時間の予測結果となります。この方法なら行列の長さや処理時間がわからなくても、待ち時間の見当をつけられますね。
人気のスイーツ店での待ち時間を予測!
具体例をイメージして考えてみましょう。
いつも行列ができている人気店でスイーツを初めて買うとして、リトルの法則で待ち時間を予測したいと思います。おおむね次のような状況だと、リトルの法則での予測に適しているとされています。先ほどの1~4の手順にしたがって、シミュレーションしてみましょう。
【状況】
- 初めて買うので、1人あたりの処理時間がわからない。
- テイクアウト専門店なので、処理時間のばらつきが少なそう。
- 行列の長さは、いつもだいたい同じぐらい。
【シミュレーション】
- 行列に加わり、1分待つ!
→時計を確認して静かに待ちましょう。 - 自分の前に並んでいる人数をざっくり数える!
→30人だったとしましょう。 - 自分の後ろに並んでいる人数を数える!
→2人だったとしましょう。 - (自分の前の人数)÷(自分の後ろの人数)を計算する!
→30÷2=15(分)
つまり、待ち時間の目安は15分ということになります。
リトルの法則での待ち時間の予測は、行列が長く安定しているほど誤差が少なくなりやすいです。そのため、規模が小さかったり処理時間が一定でなかったりすると、ずれが大きいと感じることがあるかもしれません。それでも、いつも「忙しくて行列に並ぶなんてムリ!」と見送っていた話題のスイーツも、「15分」という目安がわかれば並んでみようと判断できます。いままで諦めていたおいしいスイーツを手に入れられるかもしれませんよ。
社会で活躍する数学の考え方
リトルの法則を数学的な公式の形で表すと、おおむね次のようになります。
L=λ×W
L:待ち行列における平均処理数
λ:一定の時間あたりの平均到着数
W:すべての処理にかかる平均時間
これをW=L÷λと変形して、Wを待ち時間ととらえることで予測しよう、というのが先ほどまでに紹介した内容です。つまり、もともとのリトルの公式は処理の数量や時間の関係をシンプルに表したもので、待ち時間の予測はその応用例といえるでしょう。
ほかにもいろいろな応用例が考えられます。
たとえば、待ち行列においてサービス側の立場なら、到着数(λ)と待ち時間(W)を測って、L=λ×Wという式を使って行列の長さ(L)を計算すれば、お店の外にできる行列の管理に役立てることができますよね。
また、Lを店内にいるお客さんの人数、λを一定の時間あたりの来店人数、Wを店内でのお客さんの滞在時間とすると、W=L÷λという式を使ってお店のなかでお客さんが滞在する時間を計算することができます。この考え方をサービス側が用いることで、売り上げの向上やサービスの充実を図ることに役立てられそうですね。
さらに、工場での生産工程の管理や、道路の赤信号と青信号の時間の設定など、意外なところで応用されています。
数学を応用できれば待ち時間が充実する
待っているときにイライラするのは「あとどれくらい待つの?」と先が読めないからではないでしょうか。あるいは「離脱しようかな……、でもここまで待ったし……」と判断に迷ってしまうからかもしれません。

そんなときは少し立ち止まって、数学の考え方を活用してみましょう。リトルの法則は、世の中のいろいろな側面を助けています。きっとよい判断材料をもらえるはずです。先を読んで「待っている15分で何かしよう!」と計画的に過ごせたら、充実した待ち時間になるかもしれませんよね。
数学のすごい応用ワザで、ぜひ楽しい日々をお過ごしください!
【参考文献】
Little,J.D.「A proof for the queuing formula: L=λW」『Operations research』 9(3), pp.383-387(1961)
高橋幸雄「やさしい待ち行列(1)-図で考える待ち行列」『オペレーションズ リサーチ』40(11),pp649-654(1995)

宇津木 聡史(うつぎ さとし)
文系サイエンスライター。科学教育誌『Science Window』(国立研究開発法人科学技術振興機構発行)の副編集長などを経て、現在は単行本の執筆、出版社が発行する雑誌の記事や単行本の編集、大学や研究機関の広報物や報告書の制作などに携わっています。著書に、『似ているけれどちがう生きもの図鑑』(文一総合出版)、『おばあちゃんが認知症になっちゃった! 』(星の環会)、『教えて!科学本』(共著、洋泉社)など。