ケーキとジュースで分数の計算をやってみよう！かけ算・わり算をイチから｜ひとふり数学のチカラで日常をちょっと賢く、もっと楽しく

分数は、その意味や計算が頭のなかでイメージしにくく、苦手になりやすい内容の1つです。

しかし裏を返すと、頭のなかでイメージできれば、分数がさまざまな場面で活躍する「便利な考え方」だとわかるはず。今回は、ケーキやジュースを友達と分け合う場面を通して、分数を楽しんでみましょう。

分数は「1つのものを、何個かに等分したうちの何個分」だけじゃない！

分数とは、「1つのものを何個かに等分したうちの何個分か」を表す数です。たとえば\(\tfrac {2}{3}\)という分数は、1つのものを3個に等分したうちの2個分のことを表しています。

しかし、分数の意味はこれだけではなく、見方によってさまざまな意味ももっています。いくつか挙げましょう。

「\(\tfrac {2}{3}\)L」「\(\tfrac {2}{3}\)m」のように、測定した量の大きさ
「AはBの\(\tfrac {2}{3}\)」のように、BをもとにしたときのAの大きさの割合
わり算「2÷3」の結果（商）

当たり前のように感じるものもあれば、改めて知ったものもあるかもしれません。他にもありますが、分数には上記のようないろいろな顔があることを知っておきましょう。

また、わり算の結果を表すという意味から、わり算に成り立つ「わられる数とわる数に同じ数をかけても、わられる数とわる数を同じ数でわっても、商の大きさは変わらない」といった性質が分数にも成り立ちます。このことをもとにすると、約分や通分が説明できますね。

分数のかけ算・わり算をしてみよう！

ここから具体的なストーリーのなかで問題を解きながら、分数の計算を学んでいきましょう。

今日は、かずみさんのおうちに3人の友達が遊びに来ています。そろそろ、おやつの時間です！　4人でケーキを食べたりジュースを飲んだりするようすを、思い浮かべてください。

【分数と整数のかけ算・わり算】ケーキを分けよう！

分数と整数のかけ算

問1
昨日、お母さんが同じ大きさのホールケーキを2個買ってきてくれました。お母さんとかずみさんは、1個の\(\tfrac {1}{4}\)ずつ食べました。今日残っているケーキは何個ですか。

まずは、図に表して考えてみましょう。2人が\(\tfrac {1}{4}\)ずつ食べたので、左下の絵のような状況ですね。これを真上から見た形で表すと、右下の図のようになります。

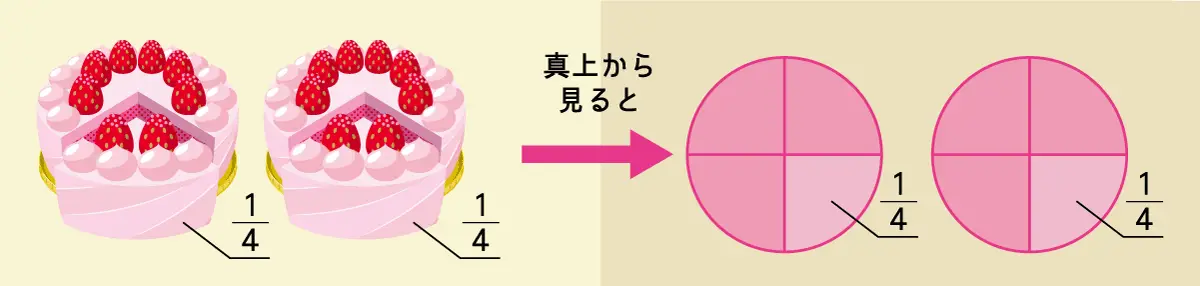
右上の図を見ると、4等分したものが6個残っていることがわかります。すなわち、\(\tfrac {6}{4}\)個です。約分すると\(\tfrac {3}{2}\)個となりますね。よって、今日残っているケーキは\(\tfrac {3}{2}\)個です。

さて、図に表すことによって答えは求められましたが、計算式だとどうなるでしょうか。\(\tfrac {1}{4}\)ずつ食べられたケーキ、つまり\(\tfrac {3}{4}\)となったケーキが2個残っているわけですから、次のようになりますよね。

\(\tfrac {3}{4}\)×2

分数と整数のかけ算が出てきました。先ほどの分数の意味に立ち返ると、\(\tfrac {3}{4}\)は「\(\tfrac {1}{4}\)の3個分」といえます。それが2個分あるわけですから、\(\tfrac {3}{4}\)×2は「\(\tfrac {1}{4}\)の（3×2）個分」となりますね。このことを式に表すことで、次のように計算できるようになります。

\(\tfrac {3}{4}\)×2=\(\tfrac {3×2}{4}\)=\(\tfrac {6}{4}\)=\(\tfrac {3}{2}\)（個）

よって、今日残っているケーキは\(\tfrac {3}{2}\)個となり、図で求めたときと同じ答えですね。

式の変わり方を見直してみましょう。かける数の2を分子の3にかけていますね。このように、分数×整数では、分子にその整数をかければよいことがわかります。このことは、文字を使って一般的に表すと、次のようになります。

分数×整数
\(\tfrac {b}{a}\)×c=\(\tfrac {b×c}{a}\)

分数と整数のわり算

問2
かずみさんは、今日残っている\(\tfrac {3}{2}\)個のケーキを4人で均等に分けることにしました。1人分のケーキは何個ですか。

こちらも、図に表して考えてみましょう。今日残っているケーキは\(\tfrac {3}{2}\)個なので、左下の図のように表せますね。これをそれぞれ4等分すると、右下の図のようになります。

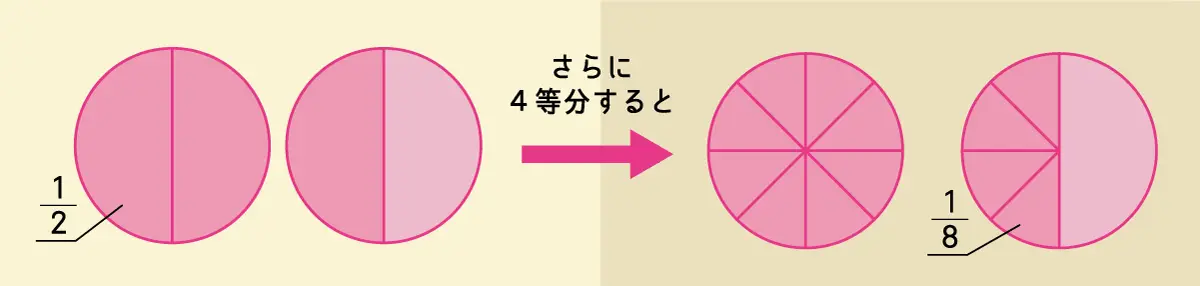
右上の図を見ると、8等分したものが12個あることがわかります。12個を4人で均等に分けると1人分は3個となりますね。よって、1人分のケーキは\(\tfrac {3}{8}\)個です。

さて、この問題でも、計算式を確認していきましょう。式をつくるのは難しくないかもしれませんね。次のようになります。

\(\tfrac {3}{2}\)÷4

分数と整数のわり算が出てきました。先ほどの分数の意味に立ち返ると、\(\tfrac {3}{2}\)は「\(\tfrac {1}{2}\)の3個分」といえます。2等分したものをさらに4等分するわけですから、\(\tfrac {3}{2}\)÷4は「（2×4）等分したものの3個分」となりますね。このことを式に表すことで、次のように計算できるようになります。

\(\tfrac {3}{2}\)÷4=\(\tfrac {3}{2×4}\)=\(\tfrac {3}{8}\)（個）

よって、1人分のケーキは\(\tfrac {3}{8}\)個となり、図で求めたときと同じ答えになりました。

こちらも式の変わり方を見直してみましょう。わる数の4を分母の2にかけていますよね。このように、分数÷整数では、分母にその整数をかければよいことがわかります。このことは、文字を使って一般的に表すと、次のようになります。

分数÷整数
\(\tfrac {b}{a}\)÷c=\(\tfrac {b}{a×c}\)

【分数と分数のかけ算・わり算】ジュースを分けよう！

分数と分数のかけ算

問3
お母さんが、ジュースが\(\tfrac {8}{3}\)L入っているビンと、4人で使うためのからっぽのペットボトルを持ってきてくれました。かずみさんは、ビンのジュースを全体の\(\tfrac {3}{10}\)だけペットボトルに移しました。ペットボトルに移ったジュースは何Lですか。

\(\tfrac {8}{3}\)Lとは、量の大きさを表す分数で、1Lを3等分したものの8個分です。すると、ビンに入っている\(\tfrac {8}{3}\)Lは、左下の図のように横線をひくことで表せますね。この\(\tfrac {3}{10}\)、すなわち10等分したうちの3個分は、右下の図のように縦線をひくことで表せます。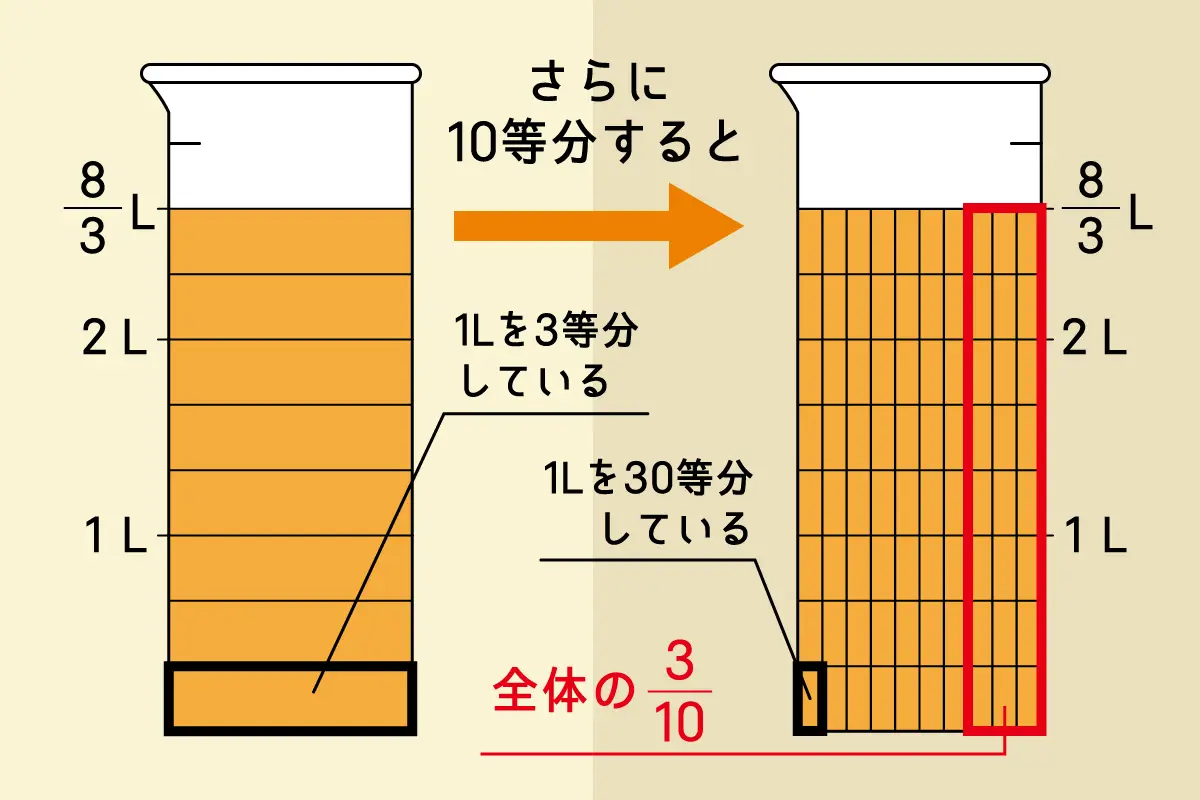

右上の図を見ると、区切られた1つの部分は1Lを30等分していることがわかります。それを24個分移すので、\(\tfrac {24}{30}\)Lとなります。約分すると\(\tfrac {4}{5}\)Lとなりますね。よって、ペットボトルに移ったジュースは\(\tfrac {4}{5}\)Lです。

計算式は、割合の計算となります。もとにする量が\(\tfrac {8}{3}\)L、割合が\(\tfrac {3}{10}\)で、比べられる量を求めればよいので、次のようになります。

\(\tfrac {8}{3}\)×\(\tfrac {3}{10}\)

分数と分数のかけ算ですね。「分数はわり算の結果を表す」という意味に立ち返ると、\(\tfrac {3}{10}\)は「3÷10」と表わせますね。このことと、先ほどの「分数×整数は、整数を分子にかける」、「分数÷整数は、整数を分母にかける」を組み合わせると、次のように計算できます。

\(\tfrac {8}{3}\)×\(\tfrac {3}{10}\)=\(\tfrac {8}{3}\)×3÷10=\(\tfrac {8×3}{3}\)÷10=\(\tfrac {8×3}{3×10}\)=\(\tfrac {24}{30}\)=\(\tfrac {4}{5}\)（L）

よって、ペットボトルに移ったジュースは\(\tfrac {4}{5}\)Lとなり、図で求めたときと同じですね。

式の変わり方を見直すと、かける数の分子の3を分子の8にかけ、分母の10を分母の3にかけていますね。このように、分数×分数では、分子どうし、分母どうしをかければよいことがわかります。このことは、文字を使って一般的に表すと、次のようになります。

分数×分数
\(\tfrac {b}{a}\)×\(\tfrac {d}{c}\)=\(\tfrac {b×d}{a×c}\)

分数と分数のわり算

問4
かずみさんは、ペットボトルに入っている\(\tfrac {4}{5}\)Lのジュースを、4人のコップに\(\tfrac {2}{11}\)Lずつ注ごうと考えています。この方法で4杯分注ぐことができますか。

問3と同じように、\(\tfrac {4}{5}\)Lは5等分したうちの4個分なので、左下の図のように目盛りをとることで表せますね。このなかに\(\tfrac {2}{11}\)Lが4個分あるかを確かめたいので、右下の図のように目盛りをとって比べればよいです。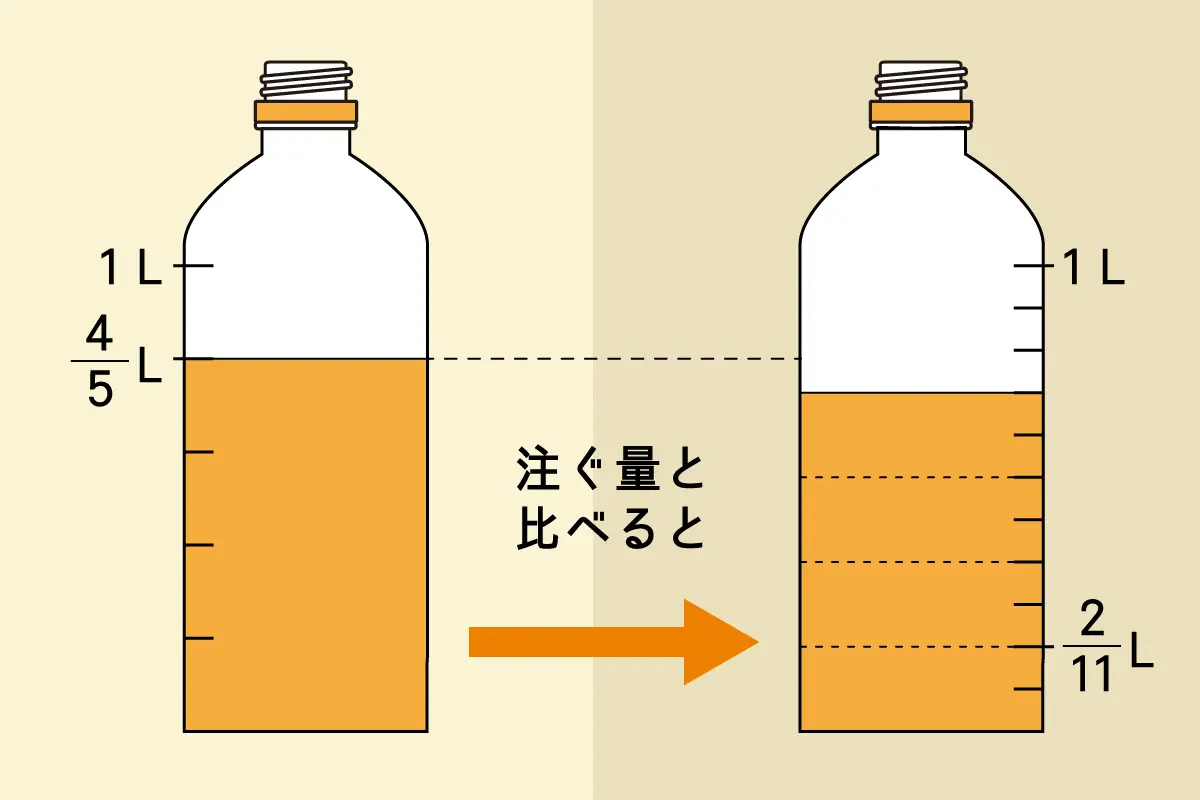

右上の図を見ると、\(\tfrac {4}{5}\)Lのほうが\(\tfrac {2}{11}\)Lの4個分より多いですね。よって、この方法で4杯のコップに同じ量ずつ注がれ、少しジュースが残ることがわかります。

計算式をつくると、次のようにわり算になります。ピンとこない場合は、簡単な場面で考えてみるとよいかもしれません。「6個のあめを2個ずつ袋に入れるとき、何袋になりますか」を求めるときの計算式は「6÷2」ですよね。

\(\tfrac {4}{5}\)÷\(\tfrac {2}{11}\)

いよいよ分数と分数のわり算の登場です。ここでは、分数がもつわり算の性質「わられる数とわる数に同じ数をかけても、商の大きさは変わらない」をもとにして考えます。具体的には、わる数の分母である11を、わられる数とわる数の両方にかけてみましょう。どうなるでしょうか。

\(\tfrac {4}{5}\)÷\(\tfrac {2}{11}\)=(\(\tfrac {4}{5}\)×11) ÷(\(\tfrac {2}{11}\)×11)=\(\tfrac {4}{5}\)×11÷2=\(\tfrac {4×11}{5}\)÷2=\(\tfrac {4×11}{5×2}\)=\(\tfrac {22}{5}\)=4\(\tfrac {2}{5}\)（杯）

これまで確認してきた、分数×整数と分数÷整数を使って求められることがわかりますね。よって商が4より大きいので、4杯分注げることがわかります。

式の変わり方を見直すと、わる数の分子の2を分母の5にかけ、分母の11を分子の4にかけていますね。このように分数÷分数では、わる数の分母と分子を逆にした分数をかければよいことがわかります。このことは、文字を使って一般的に表すと、次のようになります。

分数÷分数
\(\tfrac {b}{a}\)÷\(\tfrac {d}{c}\)=\(\tfrac {b×c}{a×d}\)

さあ、これで安心してケーキとジュースを食べられますね。

最後に1つ問題を出しましょう。問4の計算の答えは、4\(\tfrac {2}{5}\)で、4杯より多いことがわかりましたが、\(\tfrac {2}{5}\)とは何でしょうか。わり算のあまりだと思って、4杯注いだあとに残っているジュースが\(\tfrac {2}{5}\)Lなのかなと考える人がしばしばいますが、大きな間違いです。もともとジュースは\(\tfrac {4}{5}\)Lだったわけですから、半分も残っているのはおかしいですよね。

\(\tfrac {2}{5}\)とは、4杯注いだあとに残っているジュースが\(\tfrac {2}{5}\)杯分ですよということを表しています。さて、では結局ジュースは何L残っているのでしょうか。ここではあえて解説を省きますので、ぜひ考えてみてください。答えだけ伝えておきます。答えは「\(\tfrac {4}{55}\)L」です。

分数÷分数はなぜ「ひっくり返してかける」のか

ケーキとジュースを分ける場面の問題を通して、分数のかけ算・わり算を説明してきましたが、これらは説明の一例に過ぎません。

分数と整数の計算にも、分数×分数にも、他の説明のしかたがあります。とりわけ、分数÷分数については、多くの子どもがつまずくことが知られており、多くの説明が考えられてきました。

今回は、もう1つだけ、異なる説明を紹介しましょう。

問4の計算式は、\(\tfrac {4}{5}\)÷\(\tfrac {2}{11}\)でした。厄介なのは、わる数が分数であることですよね。「\(\tfrac {2}{11}\)が消えてしまえばいいのに」と、思った人も多いと思います。ならば、消してしまいましょう。\(\tfrac {2}{11}\)に対して\(\tfrac {11}{2}\)をかければよいのです。約分によって、まるで相殺されるように\(\tfrac {2}{11}\)が消えます。このとき、わる数の\(\tfrac {4}{5}\)にも\(\tfrac {11}{2}\)をかけることをお忘れなく。すると、次のような計算になります。

\(\tfrac {4}{5}\)÷\(\tfrac {2}{11}\)=(\(\tfrac {4}{5}\)×\(\tfrac {11}{2}\))÷(\(\tfrac {2}{11}\)×\(\tfrac {11}{2}\))=\(\tfrac {4}{5}\)×\(\tfrac {11}{2}\)÷1=\(\tfrac {4×11}{5×2}\)=\(\tfrac {22}{5}\)

すぐに分数×分数の式に変換されるので、わかりやすいかもしれませんね。他にどんな説明のしかたがあるか、考えてみましょう。