知って得する! 買い物じょうずな人の計算時短テク

小学校で学習する四則計算は、くふうをすればどんどん計算が速くなります。いちいち電卓を出して計算しなくても、暗算で計算することができます。ちょっとした計算でも速くできるとうれしいですよね。今回は、速く計算できる方法をご紹介します。
みなさんが日常で計算する場面というと、たとえば買い物があります。買い物で計算が素早くできるようになると、どのような選択をすればお得かの目安がすぐにわかって、買い物じょうずになること間違いなしです。
今回は、おもに買い物の場面を例にいろいろと紹介しますので、実際に問題を解きながら、1歩うえの計算力を手に入れましょう。
たし算、かけ算は順番をかえられる
まず、算数の問題です。次の計算をしてみてください。制限時間は10秒です。
1+2+3+4+5+6+7+8+9+10
どうですか? できましたか?
左から順番に計算する人もいると思いますが、ちょっとくふうすればかんたんに計算することができます。たし算は順番をかえても答えは変わりませんよね。ですから、
1+9+2+8+3+7+4+6+10+5
=(1+9)+(2+8)+(3+7)+(4+6)+10+5
=55
とすればかんたんに計算することができ、答えを求められます。これを「交換法則」といいます。キリのよい数に注目するのがポイントです。
では、これを応用して次の問題を解いてみましょう。制限時間は30秒です。
食パンが386円、あんパンが168円、クリームパンが114円で売られています。1個ずつ買うとき、代金は何円ですか。

式をつくるのはかんたんですね。
386+168+114となりますが、これも計算の順番をかえて、
386+114+168
=500+168
=668
とすればよいわけです。左から順番に計算するのではなく、キリがよくなるところから計算していきましょう。
同じように、かけ算も計算の順番をかえても答えは変わりません。
次の計算をしてみましょう。制限時間は10秒です。
1×2×3×4×5
この計算も順番をかえることでかんたんになります。たとえば、
2×5×3×4×1
=(2×5)×(3×4)×1
=10×12
=120
となります。
では、これも実際に買い物の場面で計算してみましょう。制限時間は30秒です。
1個25円のみかんが1箱に17個入って売られています。4箱買うとき、代金は何円ですか。

式をつくると、25×17×4となりますね。25×17を計算するのはたいへんですが、順番をかえて、25×4×17とするとどうでしょう。25×4=100なので、100×17=1700とすぐに計算できますね。
暗記しておくと便利なかけ算は、「25×4=100」「125×8=1000」の2つです。
次のような買い物でも計算のくふうができます。チャレンジしてみましょう。制限時間は30秒です。
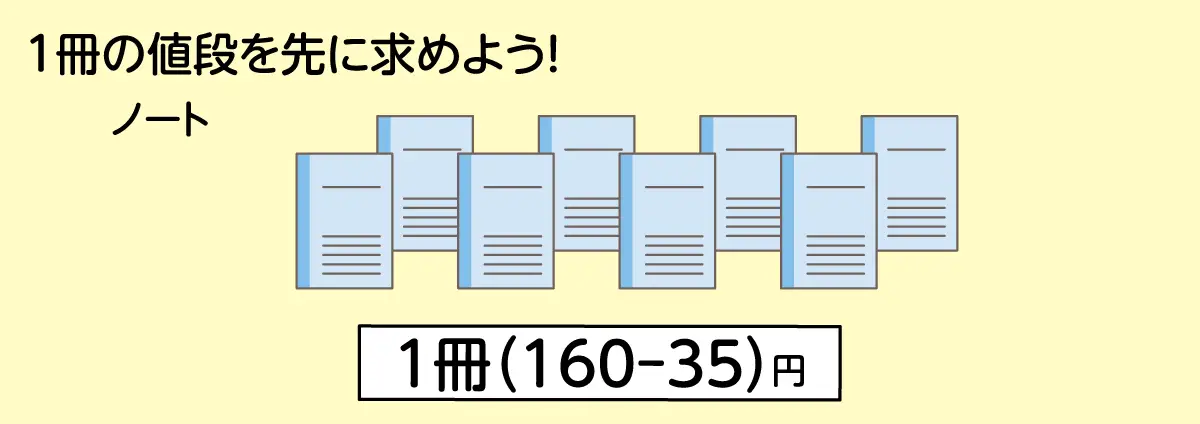
160円のノートを8冊買うとき、1冊につき35円安くしてくれました。代金は何円ですか。
式をつくると、160×8-35×8ですが、これもまとめて(160-35)×8とすると、125×8=1000とすぐに計算することができますね。このように、たし算やかけ算は、順番をかえたりまとめたりすることで素早く計算することができます。
わり算はどんどんかんたんにできる
実生活でわり算を暗算でできると本当に便利です。
まずは、基本知識の確認からしていきましょう。
次の計算をしてみてください。制限時間は10秒です。
(1) 20÷4
(2) 20000÷4000
(1)は問題ないですね。20÷4=5です。(2)はどうでしょう。そのままわり算をしてもよいですが、「わられる数(左)とわる数(右)を同じ数でわっても答えは変わらない」という性質を使います。具体的には、20000÷4000のそれぞれの数を1000でわって20÷4=5となります。
これは0がついている数でなくても使えます。84÷14という計算があれば、わられる数もわる数も偶数なので、2でわって42÷7となり、答えは6となります。このように、わり算をそのまま計算するのではなく、同じ数でわってかんたんにしてから計算すると便利です。
では、次の問題にチャレンジしてみましょう。制限時間は30秒です。
100gで268円のお肉Aと、300gで800円のお肉Bが売られています。どちらがお得ですか?
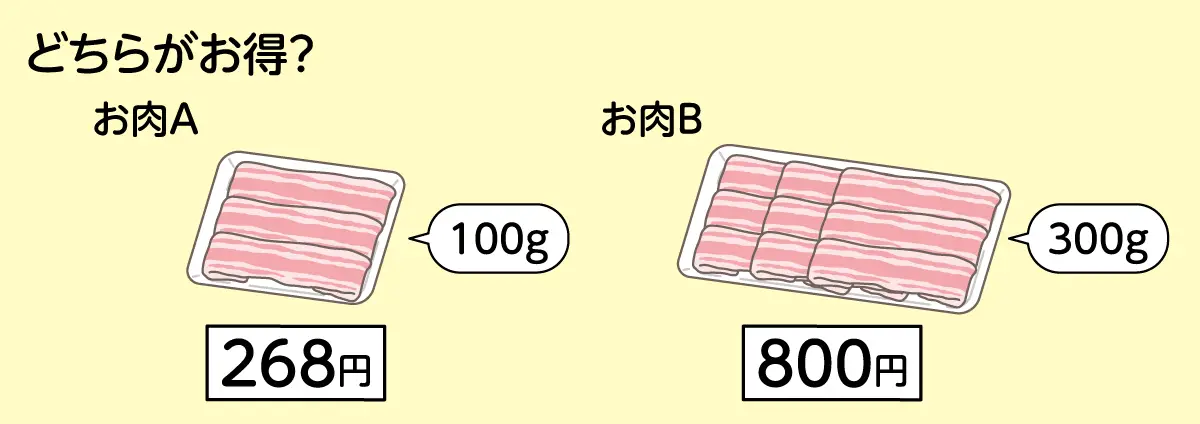
どちらがお得かを求めるときは、単位量あたりの大きさ(1gあたり何円か)を計算して比較することが多いですよね。お肉Aとお肉Bの重さが違うので、値段を比べられるようにするために、1gだと何円になるか求めるわけです。つまり、800÷300を計算することになります。
スマホを取り出して電卓アプリで計算してもよいですが、ぜひ暗算で求めてみましょう。
ここで知っておくと便利な知識を紹介します。
「÷3」の答えのあまりが「1」のとき、小数点以下は「333333……」
「÷3」の答えのあまりが「2」のとき、小数点以下は「666666……」
となることです。
まず、800÷300について、わられる数とわる数の下2ケタ「00」を消して、8÷3とします。8÷3=2あまり2なので、小数点以下は「666666……」となり、あまりを出さない答えは2.666666…となります。100gに換算すると266.6666…円なので、だいたい267円となります。
したがって、お肉Bのほうがほんの少しお得だなということがわかりますね。
ちょっとした計算のくふうを知っていると、電卓がなくても頭のなかで計算できるようになります。
単位量あたりの大きさを求めなくてもお得かどうかはわかる
突然ですが、次の問題はどうでしょうか。制限時間は30秒です。
12個入りで450円のおまんじゅうAと、8個入りで300円のおまんじゅうBが売られています。どちらがお得ですか?
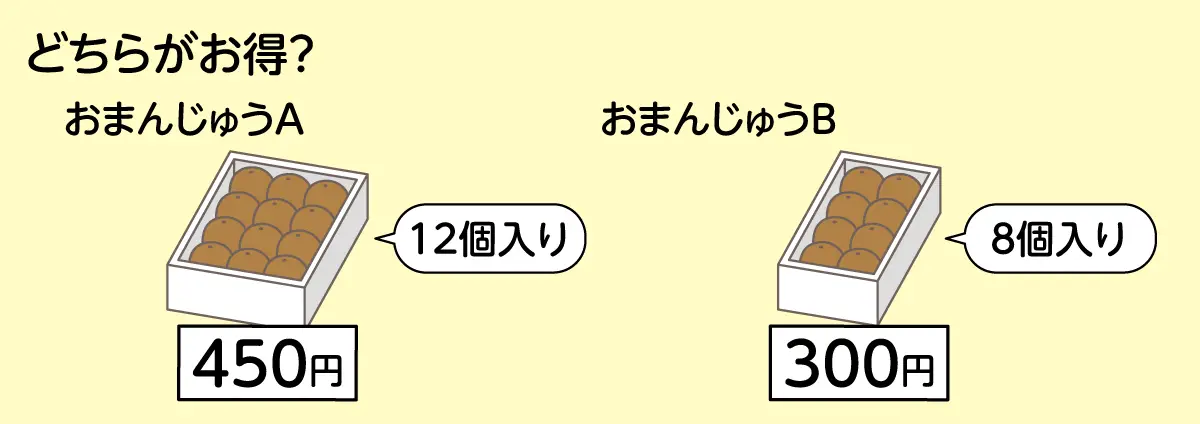
この問題も単位量あたりの大きさを求めて、450÷12=37.5、300÷8=37.5とそのまま計算してもよいですが、違う求め方があります。それは公倍数を使って、おまんじゅうの個数をそろえてから比較する方法です。公倍数とは、共通する倍数のことですね。12と8の最小公倍数は24なので、どちらも24個になるようにします。すると、
おまんじゅうA…12個入り450円→2倍して、24個900円
おまんじゅうB…8個入り300円→3倍して、24個900円
となります。どちらも900円になるので、同じとなるわけです。どうしても1個あたりの値段で求めがちですが、こういう公倍数で比べるということも一度経験しておくと、使える範囲が広がっていきます。
では、次の問題で練習してみましょう。制限時間は30秒です。
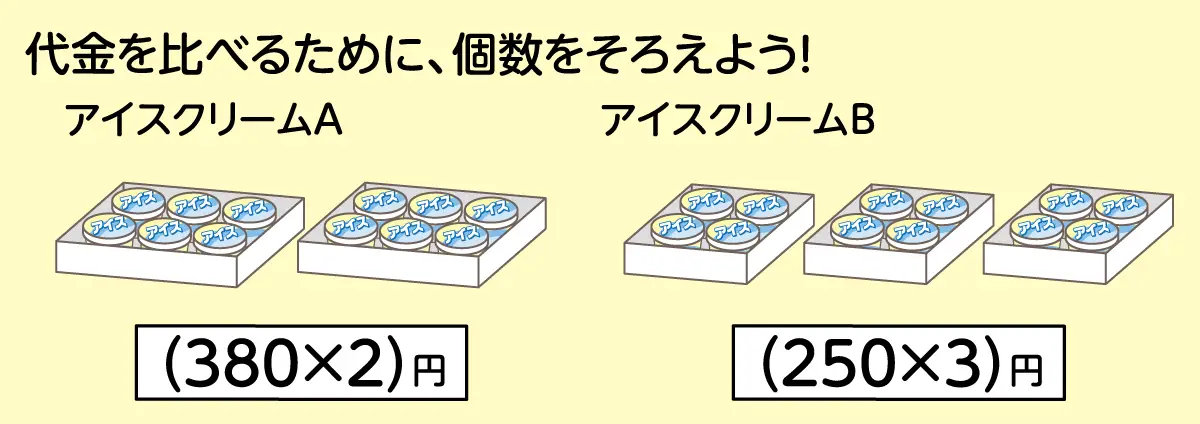
6個入りで380円のアイスクリームAと、4個入りで250円のアイスクリームBが売られています。どちらがお得ですか?
6と4の最小公倍数は12なので、どちらも12個になるようにしましょう。すると、
アイスクリームA…6個入り380円→2倍して、12個760円
アイスクリームB…4個入り250円→3倍して、12個750円
となります。したがって、アイスクリームBのほうが少し安いことがわかりますね。このように公倍数を使って、どちらがお得かを比べる方法もあります。ぜひ試してみてくださいね。
割引きの計算方法と概算という考え方
スーパーマーケットに行くと、よく「2割引き」とか「3割引き」と値札に書いてありますね。ここでは割引きについての理解を深めましょう。
まず、次の問題を解いてみましょう。制限時間は10秒です。
450円を2割引きした値段は何円ですか?
2割は小数で表すと0.2です。2割の金額は450×0.2=90となり、2割引きした値段は450-90=360となります。全体が10割なので、2割をひくと8割になることから、450×0.8=360でも構いません。
このとき、これまでやってきたように数を分解して、45×10×0.8=45×8=360としてもよいですね。
つまり、2割引きのときは、もとの値段の一の位の0を1個消して「2割引き」の「2」をかければ割引き額が計算できるのです。同じように、450円を3割引きしたときの割引き額は45×3=135円となります。
「でもそんな暗算するのはたいへんだよ」「私はそんな計算は得意ではない」という人は、概算という考え方をもっておいてください。概算というのは、おおよその計算という意味です。正確ではないけれども、だいたいこれくらいという計算のことです。
もとの数が450円だったら、だいたい500円と考えて、3割引きの割引き額は50×3=150となります。また、だいたい400円と考えた場合、3割引きの割引き額は40×3=120です。450円は500円と400円のちょうど中間なので、割引き額もだいたい150円と120円の間の値引きになることがわかりますね。だいたいの割引き額を計算できれば、どれくらいお得になるかがすぐにわかりますよね。
では、最後の問題です。制限時間は30秒です。
1980円のTシャツが2割引きで売られています。どのくらいの割引き額になりますか。概算で求めてみましょう。

概算は正確な値ではなく、だいたいどれくらいの値になるかを求めることが大事です。1980円は、だいたい2000円なので、200×2=400の値引きと考えればよいわけです。数円まできっちりと計算する方法でなくても、だいたいこれくらいになるということがすぐに計算できれば、計算はすごく楽になります。
頭のなかで計算する楽しさを
今回は、買い物を例に、さまざまな計算方法、計算のきまりを紹介しました。今回紹介した計算は、小学校で習う計算方法ばかりです。かんたんなくふうや知識で計算が驚くほど楽になります。また、単位量あたりの大きさを求めたり、公倍数でそろえたりして比較する方法もとても便利ですので、ぜひ一度使ってみてください。
まずはだいたいでよいので、電卓を使わずに頭のなかで計算することを心がけてください。頭のなかで計算をすればするほど、どんどん速く計算できるようになっていきます。頭のなかで速く計算できるようになると、今度は「状況がこうだったら結果はこれくらいだな」という計算もすぐにできるようになると思います。
今回、紹介した計算方法はあくまで例なので、他にもいろいろな計算のくふうがあります。日常生活でこんな計算のくふうをしているということがありましたら、ぜひまわりの人に話したり教えてみたりしてくださいね!

古山 竜司
大阪府生まれ。九州大学大学院卒業(芸術工学)。数学検定1級(数理技能検定)、英語検定準1級、数学コーチャープロA級ライセンス取得、ビジネス数学講師。「数学・算数を通じて人々を幸せにする」を使命に大阪府高槻市にマスラボを開業。またYouTuberとしても5,000本の動画を配信し、チャンネル登録者も1万人達成。著書に「これだけ微分積分」「これだけ微分方程式」(いずれも秀和システム)など。
算数・数学塾「マスラボ」
サイトURL:http://furuyaman.com/