日々の節約に使える投資手法とは?「ドル・コスト平均法」

いま、いろいろな商品の値段が上がっていますよね。
「また値上げか……」
買い物に行くと、そんなため息まじりのつぶやきが出てしまいます。
ただ、セールや特売、政府の支援策、世界情勢などにより価格が一時的に下がることもあります。
そんな日々、「よく買うものは、いつどれくらい購入するのがいちばんお得なのだろう?」と悩むことがありませんか。
投資で用いられる手法の「ドル・コスト平均法」という考え方を知ると、日々の買い物に役立てられるかもしれません。
激しい価格変動を乗り切る知恵
商品のなかでも、価格が上がったり下がったりしやすいものがあります。たとえば、ガソリンはその代表例ですね。小麦粉や砂糖などもそうです。スーパーマーケットなどでは特売品や目玉商品などでも、価格がよく変動していますよね。
よく買う商品なら、安いときにたくさん買いたいもの。でも、未来において商品の価格がどのように変化するかは、誰にもわかりません。そこで「ドル・コスト平均法」です。

ドル・コスト平均法は、投資の基礎的なテクニックの1つで、価格が上がったり下がったりする商品に対して、定期的に一定金額で買い続けるという方法です。この方法で同じものを買い続けると、価格が低いときはたくさん購入し、価格が高いときは購入する量が少なくなります。そうすると、相対的に「安いときにたくさん買えた!」というときが増えて「高いときにたくさん買ってしまった!」という失敗を減らせます。結果として購入単価が平均化されるため、長期的に見ると、毎回同じ量だけ買う方法に比べて購入単価を低く抑えることができます。
ガソリンの給油でシミュレーション!
ガソリンの給油を例に、買い方をシミュレーションして、比べてみましょう。
「買い方」にもいろいろあります。一度に大量に購入する方法や、価格に応じて購入する量を変える方法などが挙げられます。しかし、ガソリンをはじめとする日常的な買い物ではあまり現実的ではありません。多くの場合、保存や手間の問題が生じてしまうからです。
今回のガソリン給油の例では、定額購入と定量購入を比較することにしましょう。定額購入がドル・コスト平均法の応用ワザです。
| 条件 | |
|---|---|
| 燃費 | 1Lあたり10km |
| 走行距離 | 1日あたり20km |
Aさんは、ドル・コスト平均法を活用して、毎回定額で給油します。仮に3,000円で固定するとして、10日ごとにガソリンを入れるものとします。
Bさんは、ガソリンが少なくなってきたら満タンに給油します。仮に毎回45Lの給油として、25日ごとに購入するものとします。

では、この2人が2021年1月1日からガソリン満タン状態の自動車を使い始め、2年たったらどうなるでしょうか。当時の実際のガソリンの単価をもとにシミュレーションしてみます。
2年間の給油のデータを表にして、それぞれ簡易的に3軸のグラフにしてみました。青色が単価、赤色が給油量、緑色が支払額を表しています。
\表をご覧になりたい方はこちら/
https://www.su-gaku.net/common/hitofuri/pdf/dollar-cost-averaging.pdf
上記の2つの表の単価は「石油製品価格調査 給油所小売価格調査(ガソリン、軽油、灯油)」(経済産業省 資源エネルギー庁) https://www.enecho.meti.go.jp/statistics/petroleum_and_lpgas/pl007/results.htmlhttps://www.enecho.meti.go.jp/statistics/petroleum_and_lpgas/pl007/results.html の結果をもとにしています。
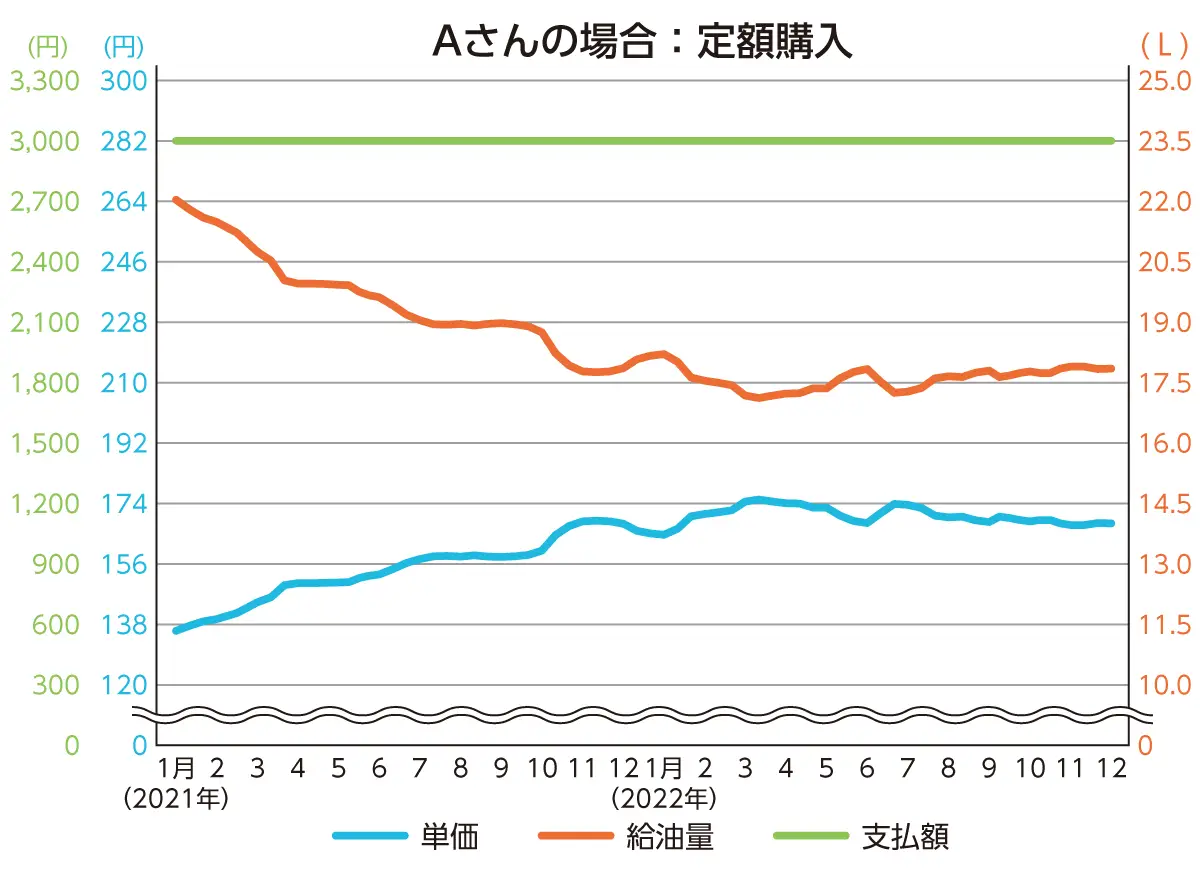
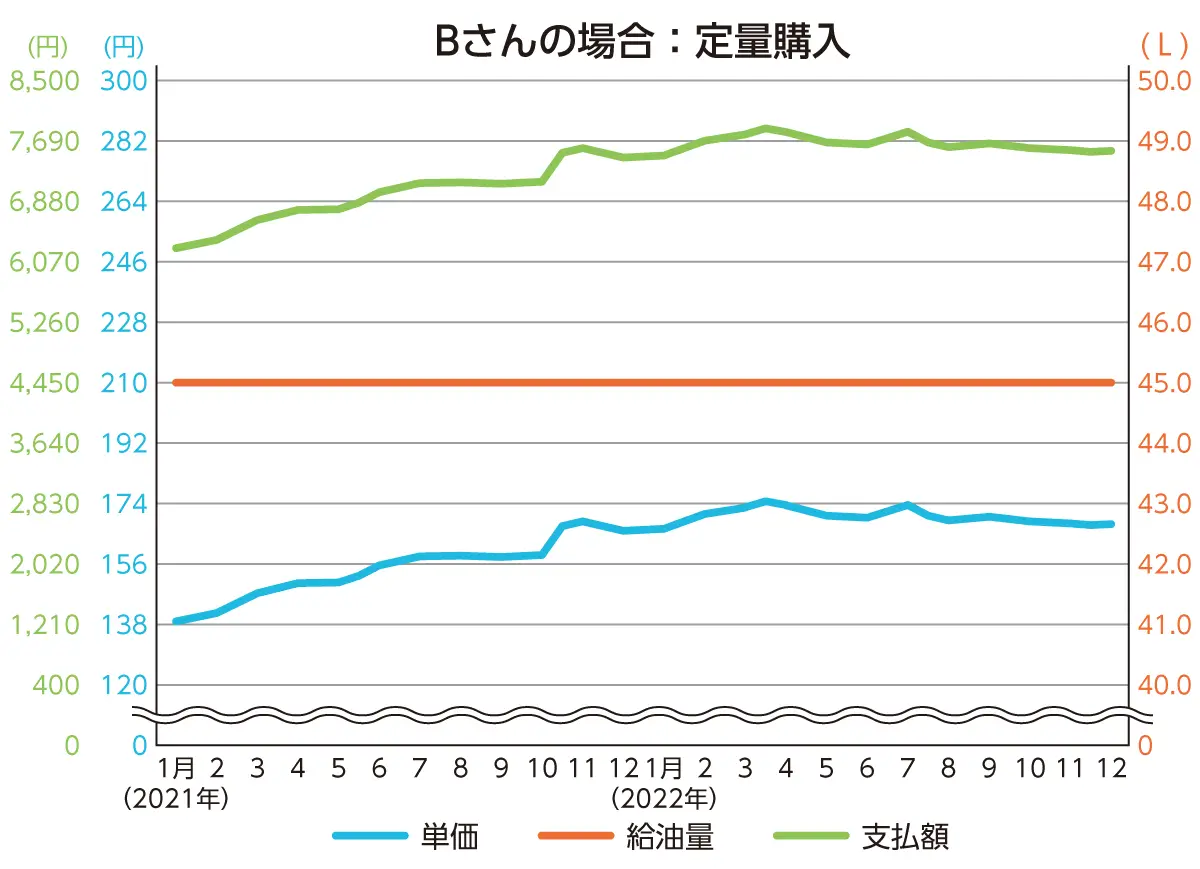
グラフを見ると、Aさんは、支払額が一定で、単価の上下に応じて給油量が逆の動きになっていることがわかります。Bさんは、給油量が一定で、単価の上下に応じて支払額が似た動きになっていることがわかります。グラフからも、Aさんは単価が安いときに比較的多く給油していることが読み取れますね。
2年間の結果を計算し、整数値になるよう処理したところ、次のようになりました。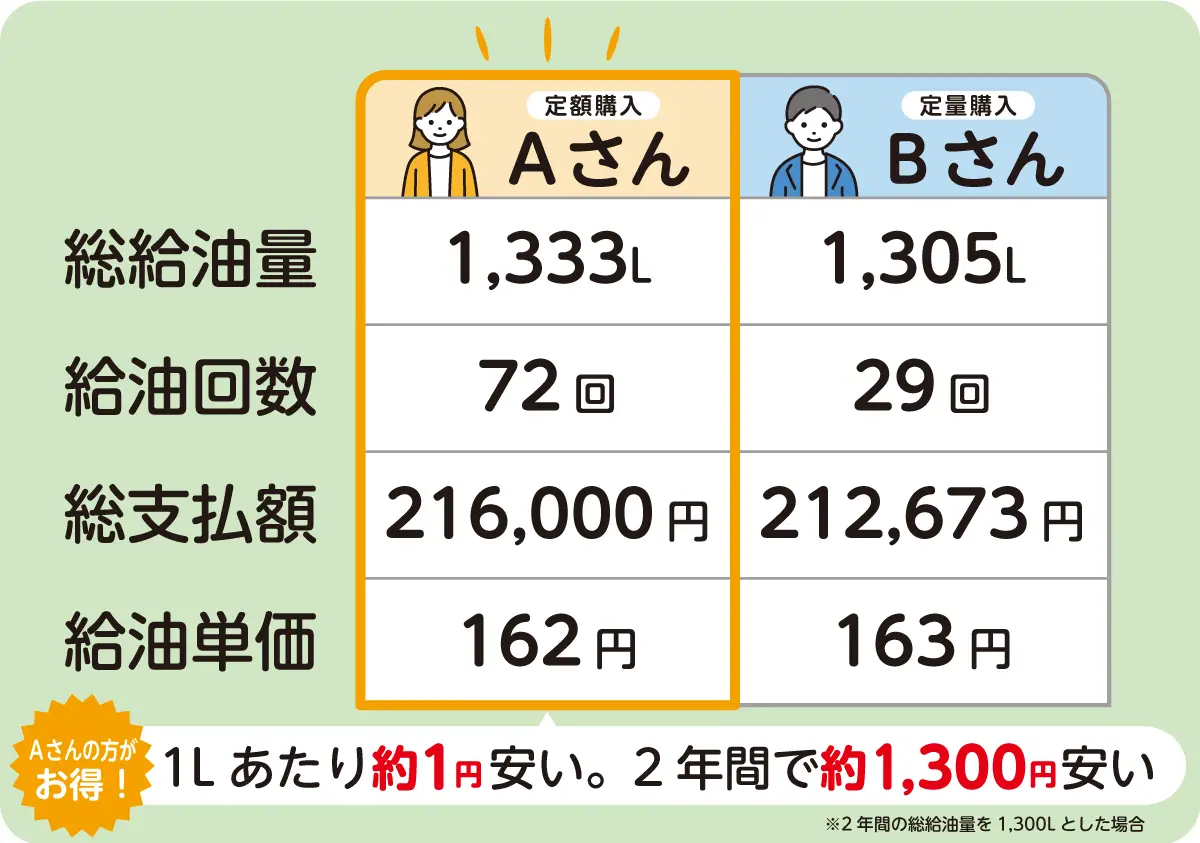
Aさんのほうが1Lあたり約1円安く給油できることになり、2年間での総給油量を1,300Lとすると、約1,300円お得になるといえる結果でした。
この違いをあなたはどう見ますか?
もともとドル・コスト平均法については、短期間でのメリットは小さく、長期間続けることで効果が出てくることが知られています。毎日の買い出しや、価格変動が激しい商品の継続的な購入など、自分の生活に照らして効果が見込めるときに上手に用いるのがよいかもしれないですね。
先行きが見通せない状況で活用される数学
今回紹介したドル・コスト平均法は、投資手法の1つとして知られています。外貨や株などの金融商品は価格が上下しますが、長期間にわたって定期的に定額で買い続ければ購入単価を抑えることが期待できます。絶対に損をしないとはもちろんいえませんが、投資リスクを低減する有効な方法とされています。
このドル・コスト平均法は、平均や重みづけといった数学の考えを応用することで、簡易的な傾斜配分を実現しています。投資などの不確定な世界でも数学は活用されているのですね。
そうして確立された手法が、私たちが暮らしている先行きの不透明な現実に新たな選択肢を与えてくれるかもしれない、というお話でした。数学は、不透明な未来を明るく照らしてくれるものでもあるのです。
※傾斜配分→配当金や予算などを均等に配分するのではなく、実績や現状などから判断して、それぞれに割り当てられる量を決めること。
【出典】
「石油製品価格調査 給油所小売価格調査(ガソリン、軽油、灯油)」(経済産業省 資源エネルギー庁)
https://www.enecho.meti.go.jp/statistics/petroleum_and_lpgas/pl007/results.html (2023年2月2日に利用)
【参考文献】
酒井富士子『キーワードでまるごとわかる投資の教科書』学研プラス(2022年)
小学館編『大辞泉 第二版』小学館(2012年)

宇津木 聡史(うつぎ さとし)
文系サイエンスライター。科学教育誌『Science Window』(国立研究開発法人科学技術振興機構発行)の副編集長などを経て、現在は単行本の執筆、出版社が発行する雑誌の記事や単行本の編集、大学や研究機関の広報物や報告書の制作などに携わっています。著書に、『似ているけれどちがう生きもの図鑑』(文一総合出版)、『おばあちゃんが認知症になっちゃった! 』(星の環会)、『教えて!科学本』(共著、洋泉社)など。